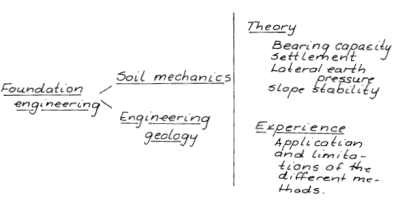
I was intrigued by Purdue University’s Rodrigo Salgado’s “Forks in the road: decisions that have shaped and will shape the teaching and practice of geotechnical engineering.” It comes at a timely point in my own journey in geotechnical education: as I write this response, I am in the process of finishing up and putting a wrap on my last semester of teaching geotechnical courses at the University of Tennessee at Chattanooga. I will explain more about this at the end of the piece but it will probably be the last time I teach these topics “face to face.”
My effort in geotechnical education has never been strictly about the classes I teach at the University. This website has enabled me to disseminate information on the topic for many years, which is implicitly educational. In more recent times I have posted topics of interest, many of which have emerged from my teaching, and I will continue that practice.
With that introduction out of the way, I can proceed to respond to the various topics that Salgado brings up.
Empiricism, science and geotechnical design
As the scion of one of the oldest active families in the business–the Vulcan Iron Works–I feel I am in an interesting position to address this issue. The Warrington-Vulcan hammer was introduced in the late 1880’s into a world where wood piles–the same types of piles driven by the Lake Dwellers in Switzerland–were pretty much the norm. It was also the era when the Engineering News formula (itself an empirical project) came into being. In subsequent years many other types of piling were introduced, but as Salgado notes soil mechanics–with the exception of lateral earth pressures–were pretty much undiscovered territory. Pile dynamics suffered from a similar level of ignorance, one compounded by civil engineers’ historic aversion to things that move. Vulcan was aware of the problems with the dynamic formulae, but it wasn’t until after World War II that these problems were tackled with a more scientific approach, and even then one gets the impression that Smith’s choice of soil model was fortuitous as much as anything else. In the meanwhile Salgado’s statement that “There is a common misconception that all engineering done before the advent of science was conservatively done” was a misconception not shared by those who really understood the problems with the pile dynamics of the first half of the twentieth century.
The Original Sins of Mohr-Coulomb and the Associated Flow Rule
I have to confess that my thinking on these topics has been formed by two processes: 1) my years of teaching a discipline where the topics do not have as immediate an integration one to another as other branches of civil engineering, and 2) my dissertation, which wasn’t complete until 2016. The latter involved writing geotechnical finite element code from the ground up, which gives me something of a greater appreciation for the issues which Salgado brings up than many who teach this course on an undergraduate level.
Let’s start with Mohr-Coulomb itself: I used it in my FEA code with the following justification:
Based on this and the elasto-plastic discussion, the Mohr-Coulomb failure model was chosen. As Abbo et.al. (2011) point out: “The Mohr–Coulomb yield criterion provides a relatively simple model for simulating the plastic behavior of soil. Other more sophisticated constitutive models for predicting the behavior of soil have been developed over the past three decades, however the complexity of these models, as well as the additional testing required to determine the various soil parameters involved, minimizes their utility for practicing geotechnical engineers. The Mohr–Coulomb yield function is also of importance to finite element researchers and practitioners as it forms the basis of many analytical solutions. These analytical solutions serve as crucial benchmarks for validating numerical algorithms and software.” This observation is supported by McCarron (2013).
In spite of its limitations, Mohr-Coulomb still has its place in geotechnical engineering. Salgado focuses on two serious problems with Mohr-Coulomb: the sharp division between cohesionless and cohesive soils and the use of the associated flow rule, an issue which doesn’t emerge in many “closed form” solutions but is certainly an important one in finite element code.
To illustrate my own journey with the first problem, having come from a deep foundations background, I was taught the cohesionless/cohesive dichotomy which is built into the whole “alpha/beta” method business. That was challenged by John Burland a long time ago. The key to ditching alpha methods–and by doing this use beta methods–is to note that the cohesion of a soil is a function of its effective stress (and other variables.) It is for this reason why I have not taught alpha methods for driven piles for some time but prefer Fellenius’ Method, recognising that the student may find themselves forced to use another method once “in the wild.” (One of these days we’ll fix that dichotomy embedded in O”Neill and Reese’s method for drilled shafts.) Fellenius’ Method has its own problems (it requires the student to use some judgement, which they haven’t quite developed) but I think in the end beta methods will win out.
But there is a more compelling factor at work: the most important single factor in the behaviour of a soil is its grain size distribution. With this soils don’t neatly divide themselves into two categories; it’s a continuum from coarse-grained to fine-grained soils. Even the classification system doesn’t quite do this justice; it’s hard to argue that a soil with 51% fines is that much different (all other things being equal) to one with 49% fines, even though they will have different classifications and the former will be considered “cohesive” and the latter “cohesionless.”
Looking at things this way, “purely” cohesive or cohesionless soils–each at the extreme of grain size distribution–are rare exceptions rather than the rule. This means that, from a Mohr-Coulomb standpoint, virtually all soils have a non-zero and
, something that Salgado notes engineers figured out a long time ago (erroneously, in his opinion.) But that’s just the beginning of the problem, we must now deal with the other quantity that Salgado brings up: dilatancy. And that in turn leads us to the business of the associated flow rule.
Once again my position on that topic is in my dissertation:
Except for purely cohesive soils, a purely associated flow rule is to be avoided for soil materials in the model. Such a rule is acceptable for many engineering materials but does not realistically model the dilation of soils, especially cohesionless ones. The downside to this is that the elasto-plastic constitutive matrix is non-symmetric, which, strictly speaking, will result in a non-symmetric stiffness matrix, increasing the cost of the problem solution.
With an associated flow rule and the dilatancy is “locked” into the value of the friction angle. With a non-associated rule
and we must determine the value of
. The literature on meaningful values of
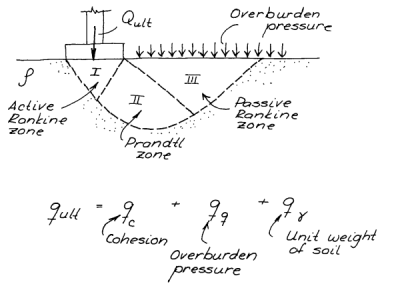
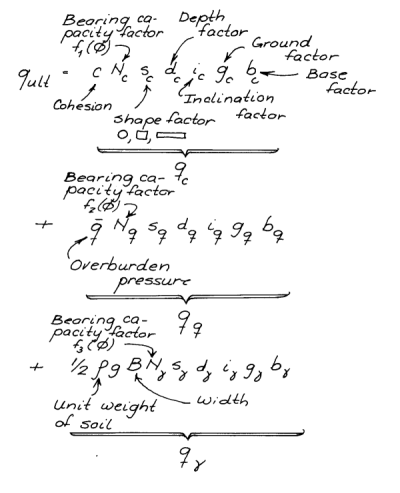
isn’t as copious as one would like but the situation is improving. Including the dilatancy solves many of the problems that Salgado raises with the Mohr-Coulomb failure criterion, especially the sole reliance on the Mohr-Coulomb failure function. (An implementation of such a rule is here.) His application of a non-associated flow rule to the bearing capacity problem is intriguing, and would be more intriguing except for the fact that generally settlement is a more important failure mode to consider than bearing capacity. (Application of this to Coulomb and log-spiral failure of retaining walls is another matter altogether.)
At this point we run into the serious problem: how to implement the solutions properly in the class setting. The problem we have in geotechnical engineering is that, in order to consider the effects of elasticity (assuming that exists, which is problematic,) plasticity and dilatancy in “one shot,” you really need finite element code, which can move from elastic to plastic deformation continuously. Most of the “hand” solutions we’ve used up to now have assumed either an elastic state or a plastic one, and the latter with an associated flow rule, as Salgado observes. I think that, moving forward, we need to consider numerical methods as the best way to solve problems in this profession. But it is dangerous to rely on these solely; they tend to become “black boxes” in the hands of many practitioners, whose results are taken as “final” even when they are erroneous. (Those of us involved in pile dynamics are all too aware of this problem.) The hand solutions in these cases need to be ancillary to make sure we are not doing something really stupid with the numerical ones, and I think our education needs to reflect that.
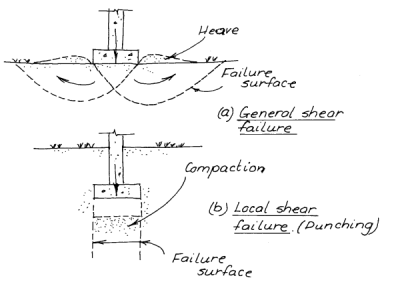
Shear Strain Localisation
The way I have dealt with this issue is to use the lower and upper bound concept, one which I have borrowed from Verruijt. By showing that there is a beginning of failure in the “surface” (a term Salgado objects to) and an end we can bracket the beginning and the end of plastic failure, which shows a truth students need to get used to in soil mechanics: our designs inherently have a degree of failure; the question that remains is how much is acceptable. Some of Verruijt’s examples of lower and upper bound are lame but that can be fixed. It’s also interesting that Salgado picked as a primary example a driven pile. In spite of being the driven pile person I am, I would not, but perhaps that’s because we get to slope stability, lateral earth pressures and bearing capacity before deep foundations. But a more comprehensive solution to the problem would be to pitch the “bearing capacity in piles” concept altogether and base design on load-settlement, which forces us to consider the progressive failure of the shaft surface from the head down and finally the failure of the toe itself.
Since he brought up the subject of driven piles and the “groundbreaking” studies of Randolph and Wroth: in that study they included varying the modulus of elasticity as one got away from the shaft surface. It is possible to use a hyperbolic stress-strain model of the soil to vary this with the strain continuously, as I demonstrate here.
Particulate Modelling and Artificial Intelligence
One thing I’m thankful that my dissertation committee (or one member) talked me out of was particulate modelling. I think that the non-homogeneity of soils and particle shapes will make this a challenging pursuit; continuum modelling should suffice for the foreseeable future.
Salgado is spot on about using any kind of artificial intelligence and machine learning without inclusion of physical modelling: it will not work. Reducing our analysis to a statistical pursuit with no regard for the basic physics of the problem–ours or anyone else’s–will lead to disaster. I have commented on this in other fora and hope our community will resist the temptation of yet another type of “magical thinking” that permeates our society.
Our World In Stress
I usually reserve things like this to another site but since he brought it up:
- Our fertility rate globally is dropping. The biggest problem we have with this is that our democracies are not prepared on dealing with funding the consequences of that change. So we will not have so many people who are consuming.
- I find it difficult to understand why, since the central problem is the emission of carbon dioxide, nuclear power is not included in the solutions. The anti-nuclear movement had its genesis in the 1960’s and 1970’s, a time when the mood among many was decidedly anti-technological. It’s time for a change.
- It is ironic that the methods used by the oft-demonised oil industry are now key to offshore wind.
The second point, in a sense, leads me to why I am departing my 20+ years of teaching geotechnical engineering in a university setting. This fall, Lord willing, I will begin teaching at Lee University, my church’s institution of higher learning. They are beginning an engineering program which has not developed to the point of being discipline-specific. I think, however, that Lee needs an engineering program, its students need the option of one, and that the liberal arts centred educational system, one we inherited from the British and have had since before the Republic began, has failed us, not only in producing a leadership class totally incapable of informed decision on technological issues, but also bereft of what Antoine Arnauld and Pierre Nicole called Logic, or the Art of Thinking. Much of this is an outcome of the same era as the anti-nuclear movement; we have replaced a pursuit of understanding with a pursuit of raw power, and the end result will be that we will end up with neither.
In summary, I think that Salgado’s idea is basically a good one. In addition to what I have observed above, I think that his program will be easier to implement in a well-funded and deep-research institute such as Purdue than in places (and there are many) where geotechnical engineering is an afterthought.