vulcanhammer.net

When Semi-Infinite Spaces Aren’t, and When Foundations are Neither Rigid Nor Flexible

Posted on 4 April 202329 April 2023 by Don Warrington

In our posts Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads and Going Around in Circles for Rigid and Flexible Foundations we discussed foundations on an elastic, homogeneous half-space, mostly purely flexible. In the latter post we ventured into rigid foundations but stuck with the semi-infinite spaces. In this post we’re going to explore cases where either one of the other or both of these aren’t true.

Some Review: Purely Rigid Foundations

In Going Around in Circles for Rigid and Flexible Foundations we looked at stress distributions under circles (and strip loads for that matter.) The results can be summarised graphically below, from Tsytovich (1976).

Figure 1. Isobars in Soil under Foundations a)absolutely rigid foundation, b)flexible foundation (from Tsytovich (1976))

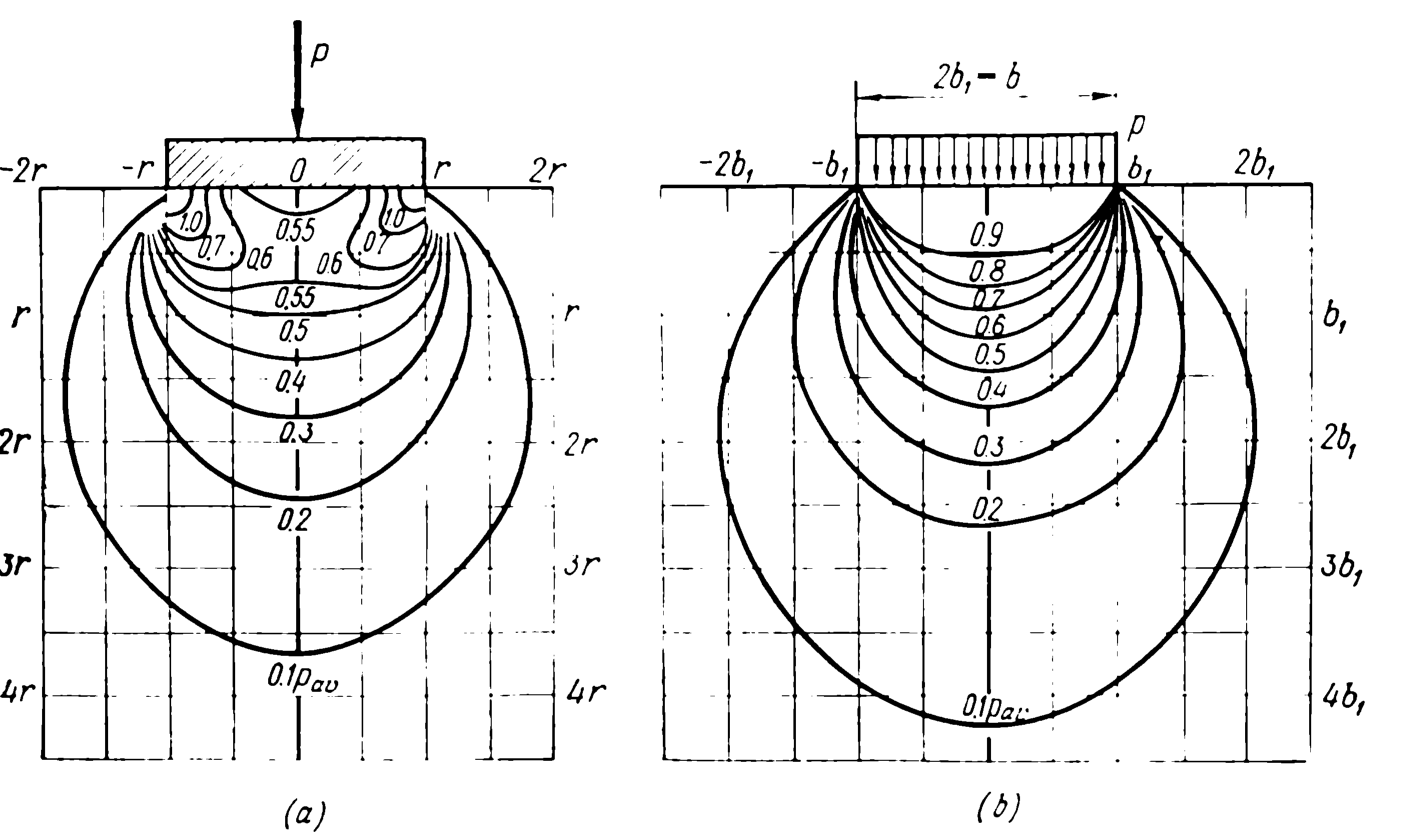
View (a) shows a point load on a rigid foundation; it could be a distributed one too, as long as the load is concentric. In any case at the corners the vertical stress is infinite. In the real world one would expect the soil to go plastic long before that and the stresses to redistribute themselves, but we’ll stick with pure elasticity for the moment.

View (b) shows a distributed load on a flexible foundation. At the interface between the foundation and the soil the vertical stress is the load p, and it decreases the further you get away from the foundation. The strip load version of this is used to find the lower bound solution for bearing capacity in Lower and Upper Bound Solutions for Bearing Capacity.

This is the state of affairs for foundations which are either perfectly flexible or perfectly rigid. The truth is that neither one of these extreme approximations is really true. This is illustrated in the figure below.

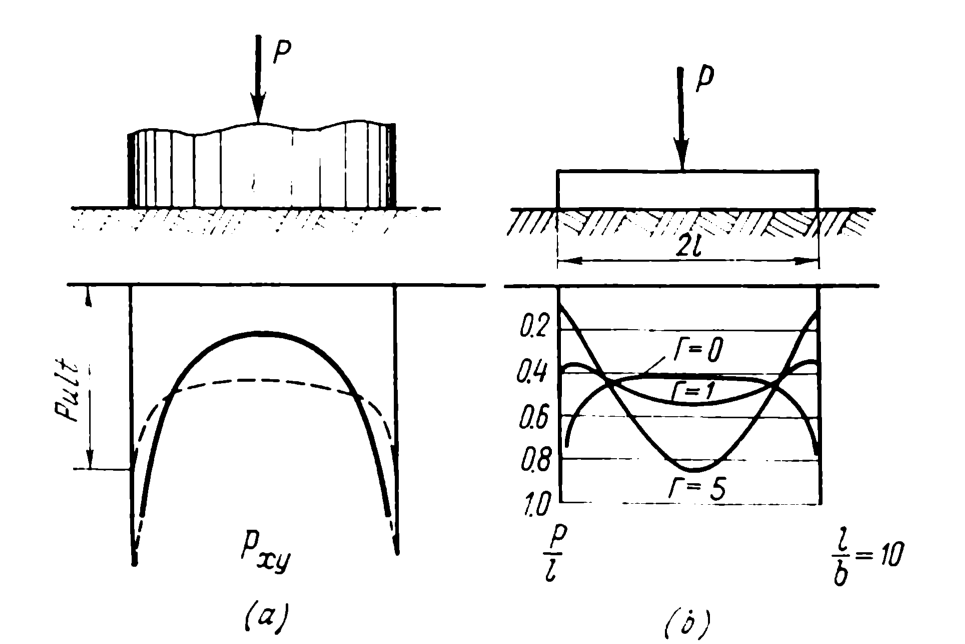
Figures 2. Diagrams of contact pressures a) under an absolutely rigid foundation, b) under foundations of various flexibilities. (From Tsytovich (1976))

View (a) shows the rigid foundation with the stresses at the base of the foundation as they would be in elastic theory (solid line) and those with some “real world” plasticity thrown in (dashed line.)

If the rigid foundation is circular, for a semi-infinite, elastic homogeneous space, the stress distribution is as follows:

$\sigma_{z}=\frac{p}{2\sqrt{1-\left(\frac{x}{r}\right)^{2}}}$ (1)

where

$\sigma_z =$ vertical stress in soil
$p =$ uniform pressure on foundation. With rigid foundations we can have a point load P and obtain the same result as long as the load is at the centroid of the foundation
$x =$ distance from centroid
$r =$ radius of foundation

The relationship between a distributed load and a point load at the centroid is

$P = p \pi r^2$ (2)

For a rigid strip foundation,

$\sigma_{z}=\frac{2p}{\pi\sqrt{1-\left(\frac{2y}{b}\right)^{2}}}$ (3)

where

$y =$ distance from centreline of strip load
$b =$ width of foundations

If we define, as is done in Figure 1, the half width of the foundation as

$b_1 = \frac{b}{2}$ (4)

then Equation (3) becomes

$\sigma_{z}=\frac{2p}{\pi\sqrt{1-\left(\frac{y}{b_1}\right)^{2}}}$ (5)

The line load can be computed as follows:

$P = p b$ (6)

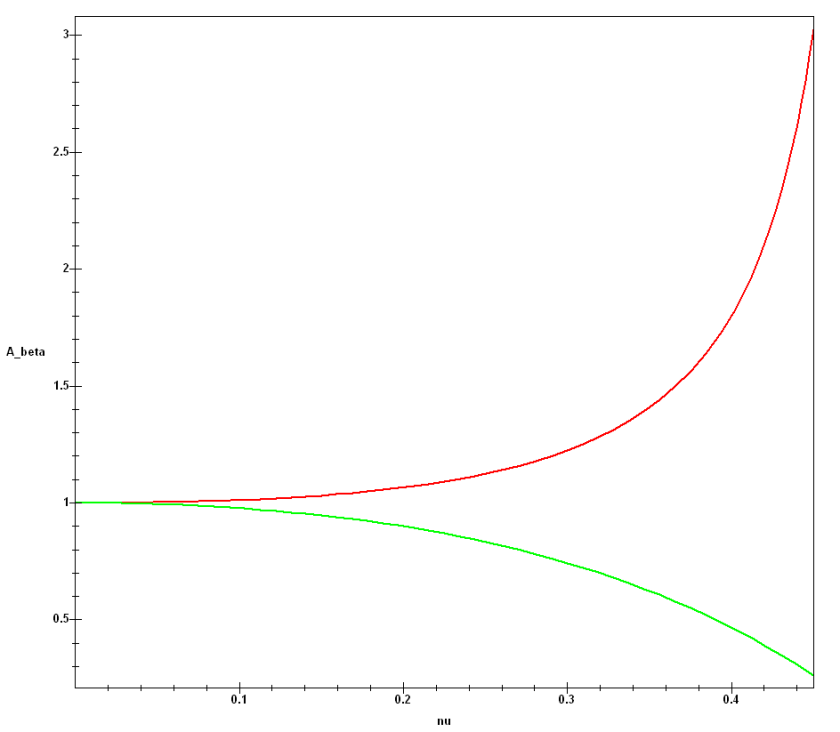
View (b) shows a foundation with varying flexibility and the effect that has on stress distribution at the base. The flexibility of the foundation is described by the variable $\Gamma$ . We’ll discuss how that’s calculated later but $\Gamma$ is a measure of the flexibility of the foundation.

$\Gamma = 0$ is a totally inflexible (rigid) foundation
$\Gamma = \infty$ is a totally flexible foundation.

Before we get to that, let’s take a look at the other problem, that of a non-semi-infinite half space.

Non-Infinite Spaces and Flexible Foundations

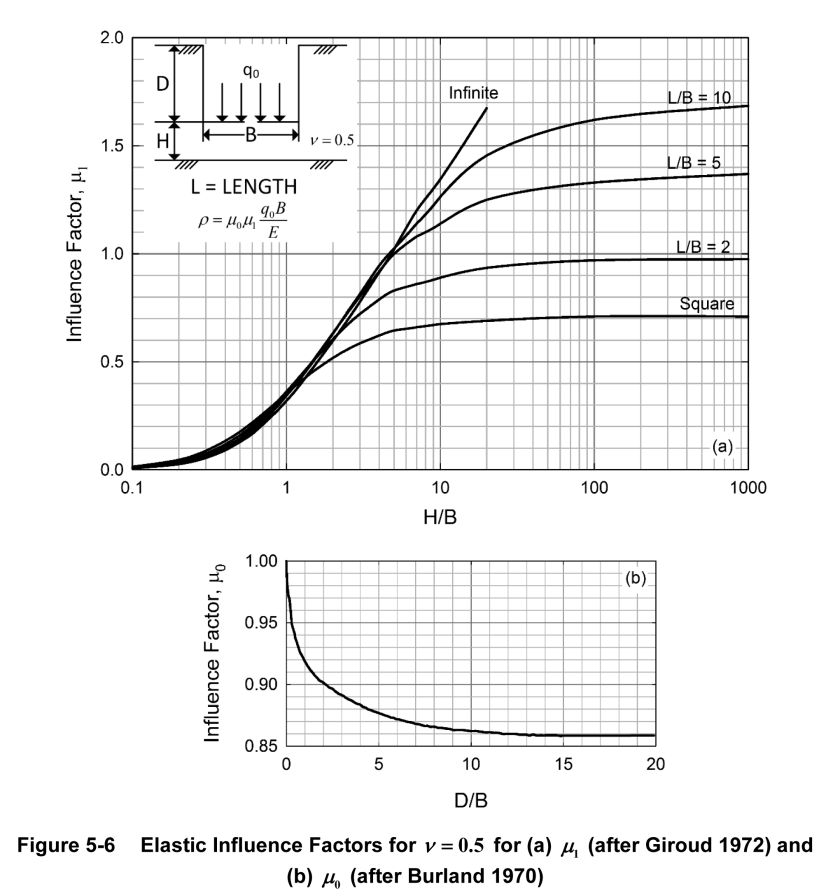
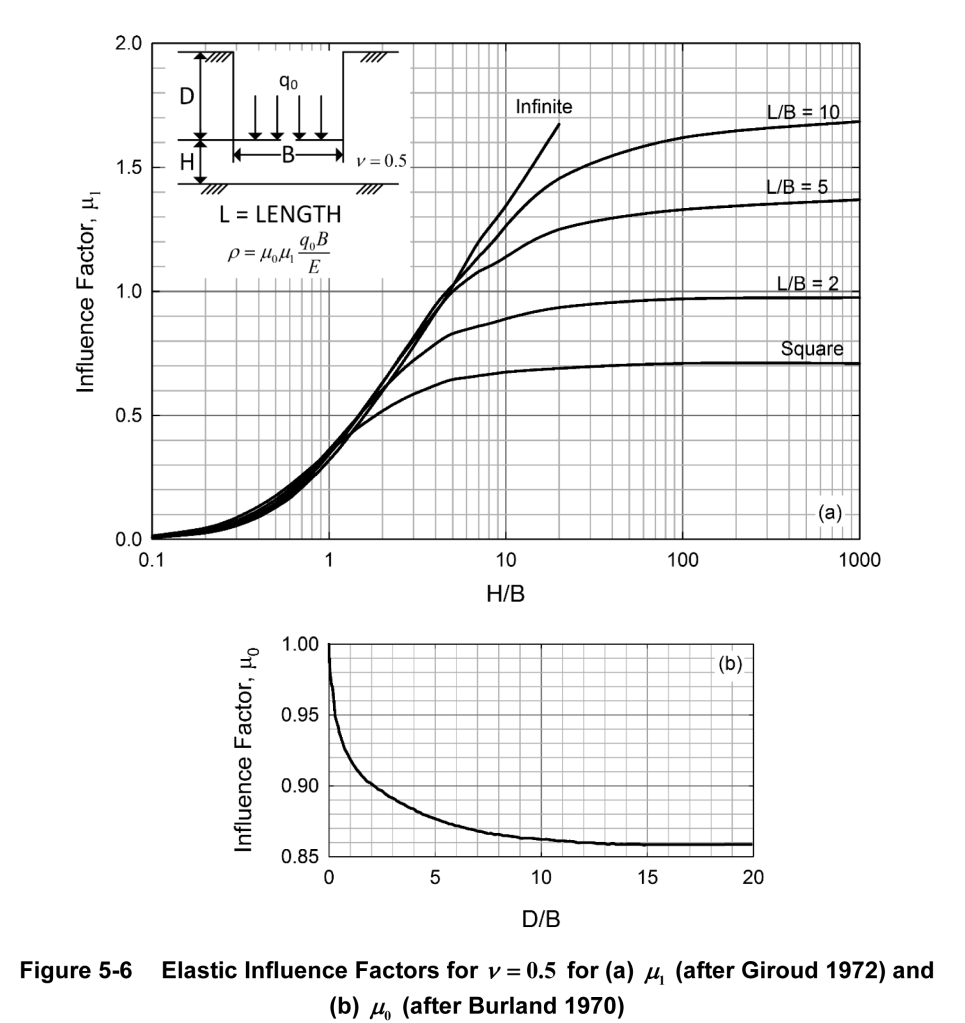
We’ll start with this problem, which is a progression from what we saw in Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads and Going Around in Circles for Rigid and Flexible Foundations. Unfortunately the state of some of our usual sources forced us to make the treatment of this topic longer than we thought, so you can see it in our post Strange Results: The Case of Settlements on Non-Infinite Elastic Half Spaces and Flexible Foundations.

Non-Infinite Spaces and Rigid Foundations

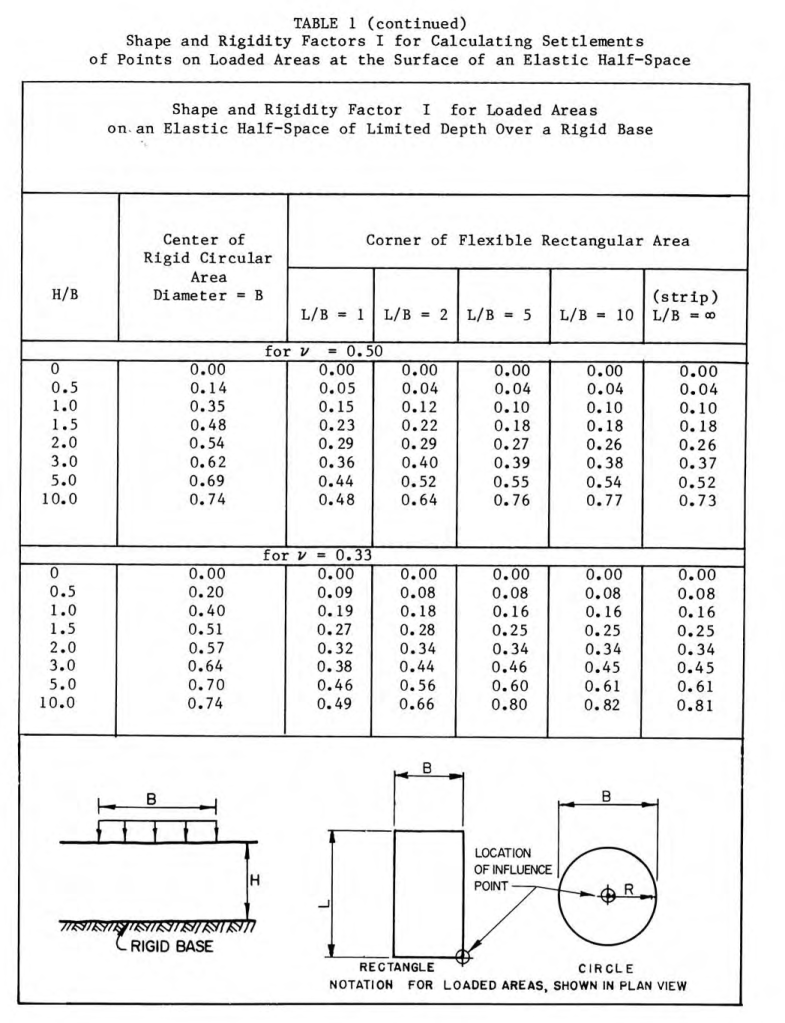
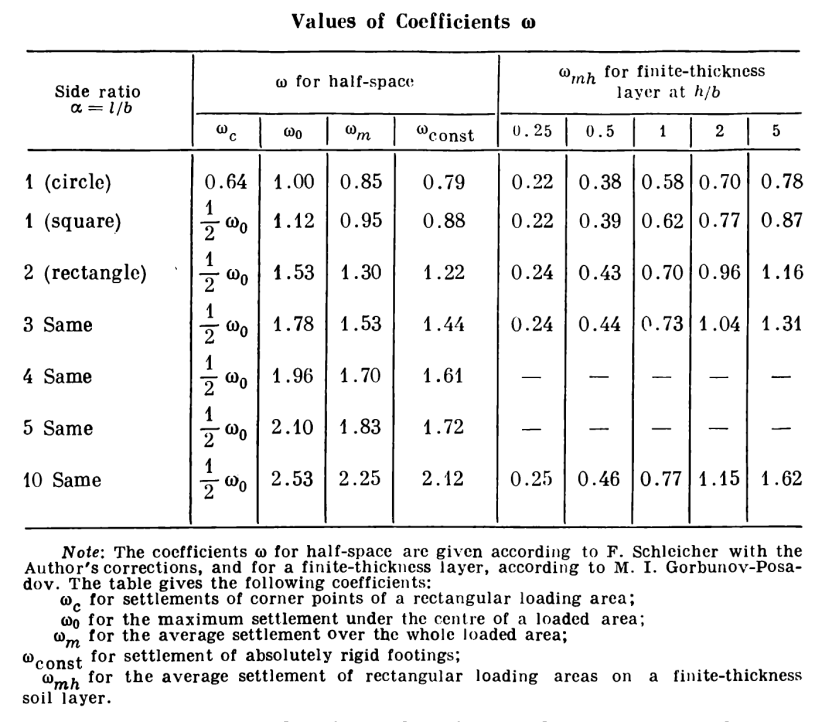
We now turn to the case of non-infinite spaces and rigid foundations. To deal with this problem we first present this table, from Tsytovich (1976):

Table 1. Contact Pressures under a Rigid Foundation on a Soil Layer of Limited Thickness (fractions of p, from Tsytovich (1976))

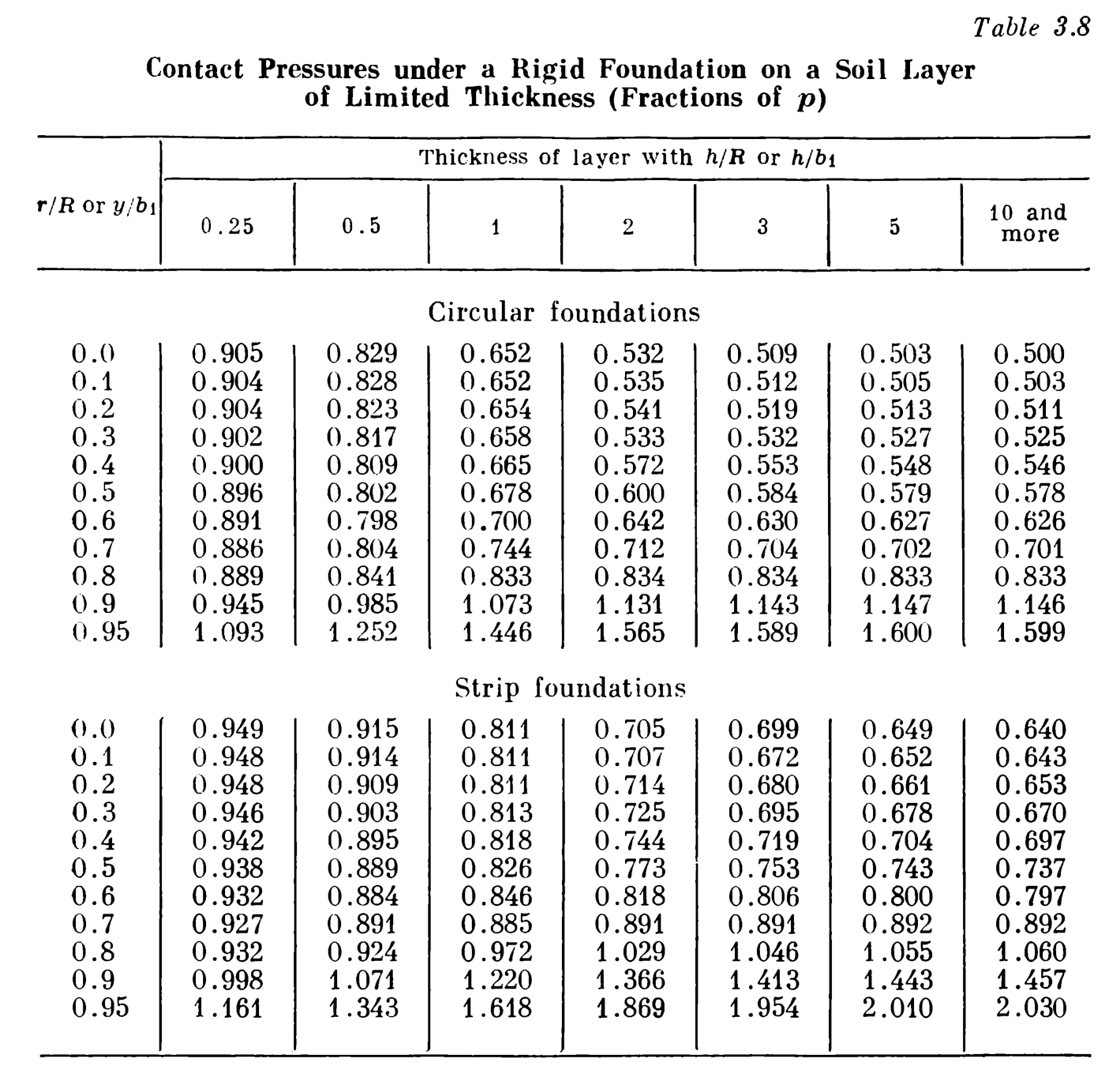
The simplest way to show how this is used is through an example. Consider the case of a rigid strip load 3m wide and having a uniform pressure p = 50 kPa. Determine the stress distribution under the soil if the layer under it (until is encounters a hard layer) is 3 m.

We start by considering Figure 1 and computing b₁ = b/2 = 1.5m. We can thus say that h/b₁ = 3/1.5 = 2. The ratio y/b₁ varies from zero (at the centre of the foundation) to 0.95 (almost to the edge of the foundation, where the stress is infinite.) We compute the results for both the limited layer depth case (using Table 1) to the semi-infinite elastic space (using Equation 5) and tabulate the results below.

y/b₁	y, m	Pressure Ratio (from chart)	Pressure, Limited Layer Depth, kPa	Pressure Ratio, Semi-Infinite Half-Space	Pressure, Semi-Infinite Half Space, kPa
0	0	0.705	35.25	0.637	31.831
0.1	0.15	0.707	35.35	0.640	31.991
0.2	0.3	0.714	35.7	0.650	32.487
0.3	0.45	0.725	36.25	0.667	33.368
0.4	0.6	0.744	37.2	0.695	34.730
0.5	0.75	0.773	38.65	0.735	36.755
0.6	0.9	0.818	40.9	0.796	39.789
0.7	1.05	0.891	44.55	0.891	44.572
0.8	1.2	1.029	51.45	1.061	53.052
0.9	1.35	1.366	68.3	1.461	73.025
0.95	1.425	1.869	93.45	2.039	101.941

Table 2. Results of Rigid Strip Load Example

The effect of the limited layer depth is primarily to flatten the pressure distribution across the base of the foundation. The pressures are greater for the limited layer depth case in the centre and less towards the edges. Inspection of Table 1 will show that this effect will become more pronounced as the layer below the foundation becomes thinner.

It is interesting to note that, while the right column is very close to Equation (5), it is not identical. The solution is shown in detail in Elastic Solutions Spreadsheet.

Foundation Flexibility

We have discussed the foundation flexibility coefficient $\Gamma$ . A general formulation of this is

$\Gamma =1/4\,{\frac {\pi \,E_{{s}}{l}^{3}b\left (1-\nu_{{f}}\right )^{2}}{\left (1-\nu_{{s}}\right )^{2}E_{{f}}I_{{f}}}}$ (7)

where

$E_s, \,\nu_s=$ Young’s Modulus and Poisson’s Ratio of the soil
$E_f, \,\nu_f =$ Young’s Modulus and Poisson’s Ratio of the foundation
$l =$ Half length of foundation
$b =$ Width of foundation
$I_f =$ moment of inertia of foundation

If we substitute

$I_f = \frac{b h^3}{12}$ (8)

then

$\Gamma=3\,{\frac {\pi \,E_{{s}}{l}^{3}\left (1-\nu_{{f}}\right )^{2}}{\left (1-\nu_{{s}}\right )^{2}E_{{f}}{h}^{3}}}$ (9)

Making common substitutions of $\nu_f = \nu_s = \frac{1}{3}$ yields

$\Gamma = 9.425\,{\frac {E_{{s}}{l}^{3}}{E_{{f}}{h}^{3}}} \approx 10 {\frac {E_{{s}}{l}^{3}}{E_{{f}}{h}^{3}}}$ (10)

which we will use in our subsequent calculations.

At this point it’s probably worth noting that relative flexibility between foundation and soil is most important in mat foundations. These days most of these will be designed using finite element analysis or some other numerical method, and rightly so. If the flexibility is more than rigid ( $\Gamma > 0$ ) the distribution of the load will come into play, and it is seldom that a foundation is uniformly loaded. In the case of eccentrically loaded foundations, even with rigid foundations the load is redistributed.

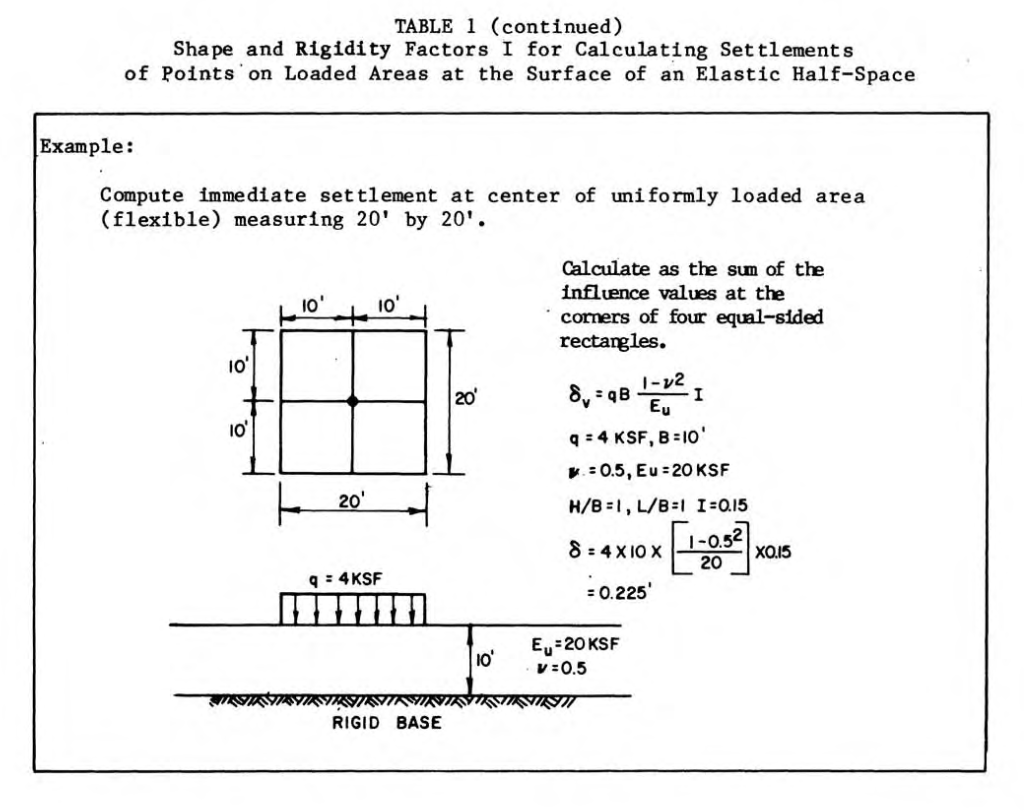
Nevertheless some kind of “back of the envelope” exercise is useful, not only for educational purposes but also for purposes of preliminary calculations. This is what we will do for stress distribution under a foundation with flexibility of $0 < \Gamma < \infty$ . To begin we will present the following table, and as before we will illustrate its use with an example.

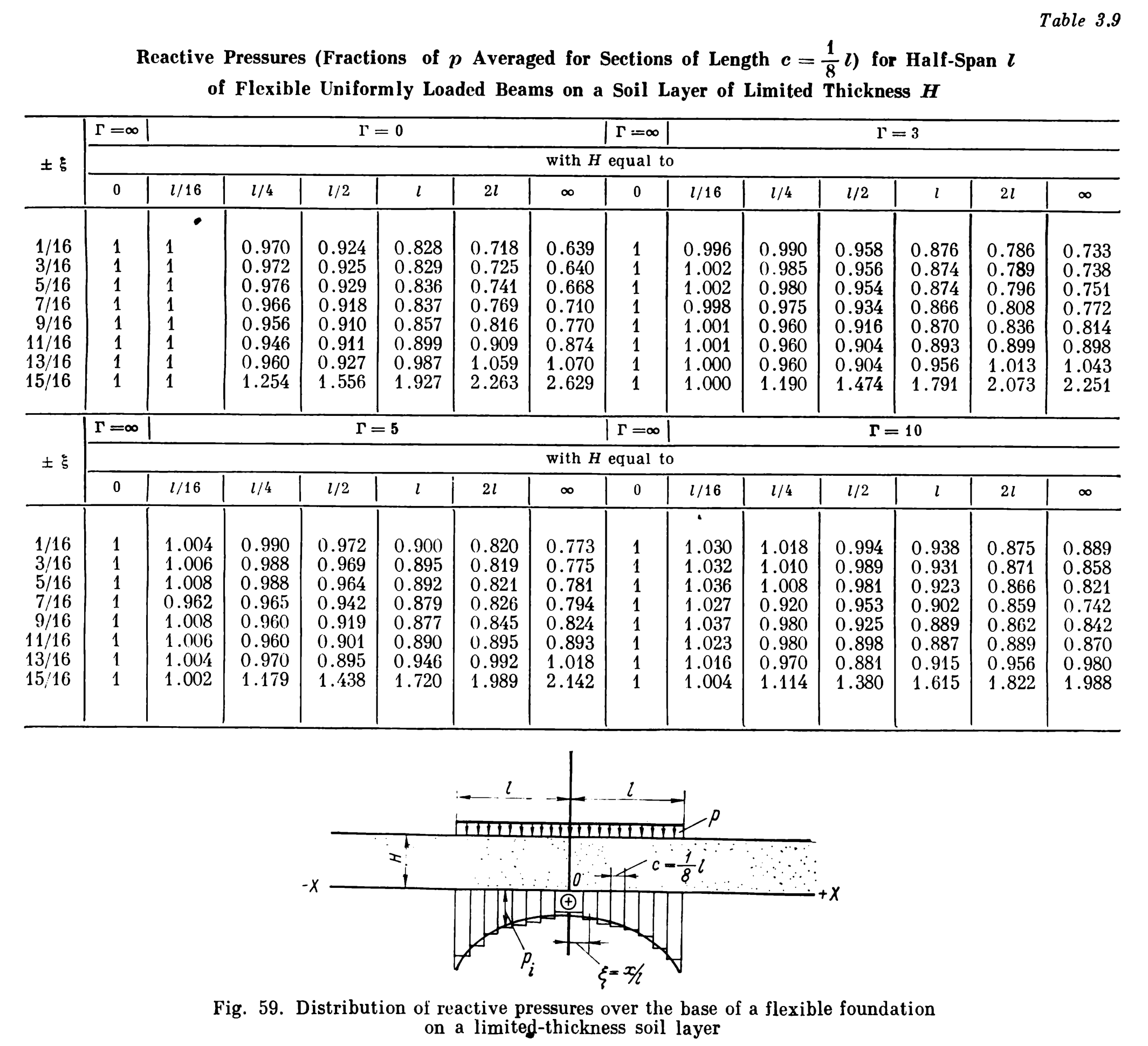
Table 2. Relative Pressures for Half-Span l of Flexible Uniformly Loaded Beams on a Soil Layer of Limited Thickness H, with a Distribution Diagram (from Tsytovich (1976))

Let’s first dispense with the columns labelled $\Gamma = \infty$ . These are purely flexible foundations, the pressure on the soil is the same as the pressure on the foundation. The rest of these are for foundations with varying degrees of rigidity, from purely rigid foundations ( $\Gamma = 0$ ) to those where, as $\Gamma$ increases, the flexibility of the foundation does also.

Since we are dealing with rectangular foundations, with a uniform pressure p the stress distribution is symmetrical about the centroidal axes of the foundation. The ratio $\xi = \frac{x}{l}$ is the fraction of the distance between the centroidal axis and the long end of the foundation, and in this case is divided into eight equal segments.

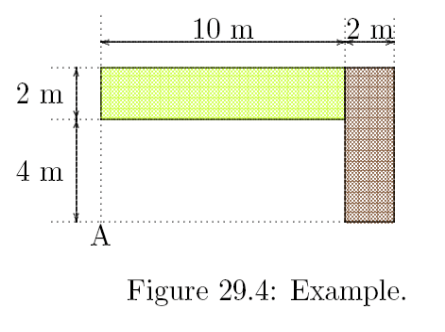
For an example, let us consider the foundation we looked at in Strange Results: The Case of Settlements on Non-Infinite Elastic Half Spaces and Flexible Foundations. It is shown below; the deflection result shown was discussed in that post.

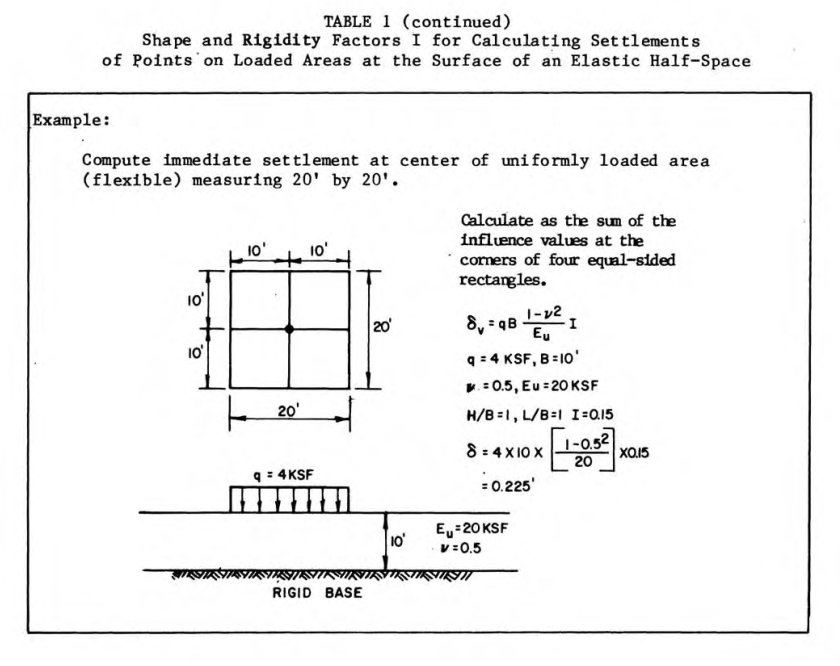
Figure 3. Example of Shape and Rigidity Factors I for Calculating Settlements of Points on Loaded Area at the Surface of an Elastic Half-Space (from NAVFAC DM 7.01)

The parameters necessary are as follows:

The Young’s Modulus for concrete is approximately 720,000 ksf.
We will assume that the foundation is 0.45′ (5.4″) thick for reasons that will become apparent.
The half length $l$ of the foundation is 10′, which means that, for Table 2, $\frac{l}{h} = \frac{10}{10} = 1$ .
We will use the approximate value of $\Gamma$ in Equation 10. Substituting, $\Gamma = \frac{20 \times 10^3}{720000 \times 0.45^3} \approx 3$ , which avoids a great deal of interpolation.

Using Table 2 and making the appropriate substitutions yields the following results.

\xi — Table 3 Results of flexibility study

\Gamma = 3 — Table 3 Results of flexibility study

From this result we note the following:

As a practical matter, the results of the rigid foundation and that for $\Gamma = 3$ are not that different, but they are different from the flexible foundation ( $\Gamma = \infty$ .)
The foundation is fairly thin to be considered “rigid.” One possibility is that the Young’s Modulus for the soil is very low. If we were to increase this by a factor of 10 to 200 ksf, we would achieve the same value for $\Gamma$ with a foundation 1′ thick, which is still rigid relative to the soil.
By the time $\Gamma = 10$ the foundation is approaching being purely flexible.

The solution is shown in detail in Elastic Solutions Spreadsheet.

Other Representations of Relative Rigidity

Although it would be nice to be able to determine the soil stress distribution under a foundation, for preliminary purposes it is probably not necessary since other methods of analysis must be done. Nevertheless the rigidity coefficient $\Gamma$ is potentially useful as a starting point to determine whether a foundation can be considered rigid or flexible.

One such use is shown in NAVFAC DM 7.1:

Table 3. Relative Mat Stiffness and Behavior (after Brown (1969,) Frazer and Wardle (1976))

A different notation for the stiffness factor is noted, but the similarity between the equations (especially that of the rectangular foundation) and Equation 10 is unmistakable. This is because there are common sources to both. For rectangular foundations the relationship between the two can be found by the equation

$K_m = \frac{\pi}{2\Gamma}$ (11a)

or conversely

$\Gamma = \frac{\pi}{2 K_m}$ (11b)

Thus, considering rectangular foundations in Table 3, a foundation is flexible if $\Gamma = 31$ , rigid if $\Gamma = 0.157$ , and intermediate between these values. For practical purposes, an intermediate foundation has $0.16 < \Gamma < 31$ , it is rigid below this and flexible above.

One interesting difference is that Table 3 uses the short dimension B while Equation 10 uses the long half dimension l. For the square foundation in the example this isn’t a problem. However, it makes sense that the longer dimension drives the flexibility–and the bending moments–of the foundation.

In any case the behavior of the foundation can be affected by the relative rigidity of the mat and the soil under it. As NAVFAC DM 7.1 notes:

As indicated in Table 5-8, mats with low stiffness ratios can be considered completely flexible. Flexible mats will apply a relatively uniform pressure distribution, and the center, edges, and corners will settle differentially. Mats with high values of $K_m$ * will act in a rigid manner and will tend to settle uniformly.
* Or low values of $\Gamma$

Two other factors need to be considered: the bending stresses in the mat (which is also affected by the reinforcement scheme) and the maximum stresses in the soil. The bending stresses in the mat needs to be considered on a case-by-case basis. Conventional wisdom may indicate that rigid mats would have larger bending stresses, but flexible mats are probably relatively thin and bending stresses may increase in these cases. The maximum stress in the soil immediately around the mat are higher with rigid mats than with flexible ones, especially along the edges. However the soil stresses that most influence the behaviour of the mat may be those which induce the largest settlements, such as those in, say, soft clay layers.

Strange Results: The Case of Settlements on Non-Infinite Elastic Half Spaces and Flexible Foundations

Posted on 30 March 20233 September 2023 by Don Warrington

In our earlier post Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads we discussed the stress under and settlement of foundations (mostly flexible) on a semi-infinite half space. Usually, though, a hard/competent layer intervenes to mess things up. Some of the books offered on this site–in print and download–have solutions for this problem. Unfortunately unexpected things happen when we consider these things carefully.

To illustrate this, let’s start with the table and diagram below, from NAVFAC DM 7.01.

Table 1. Shape and Rigidity Factors I for Calculating Settlements of Points on Loaded Area at the Surface of a Limited Elastic Half-Space (from NAVFAC DM 7.01)

The settlement at the centre of the full foundation (sum of the corners of the divided foundation, see below) is given by the equation

$\delta_v = NqB' \frac {1-\nu_s^2}{E_s} I$ (1)

where

$N =$ number of partial foundations used to compute total settlement (with centre settlements, usually $N = 4$
$q =$ uniform load on foundation
$B' =$ small dimension of partial foundation
$\nu_s =$ Poisson’s Ratio of soil
$E_s =$ Young’s Modulus of soil
$I =$ influence coefficient

Note that we’re now dealing with settlements. The soil being compressed is limited to a height H from the surface to the “rigid base.” In this diagram we do this corner by corner, as we did for the stresses in Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads. In both this and Going Around in Circles for Rigid and Flexible Foundations we used another chart, which is shown below.

Table 2. Values for the influence coefficients omega (from Tsytovich (1976))

The two charts differ as follows:

Both use Equation (1), albeit differently, as described immediately below.
The basic formula is the same but the influence coefficient notation is different; the DM 7.01 chart uses I while the Tsytovich chart uses $\omega$ .
The settlement is presented differently; the DM 7.01 chart shows it at the centre of the circular foundation and the corner of the rectangles while the Tsytovich charts shows an average settlement. For the Tsytovich chart, the dimension B’ should be replaced by b, the full small dimension of the foundation, and L’ by l, the full large dimension of the foundation. In this case $\alpha = \frac{l}{b}$ .

Let us look at an example, from NAVFAC DM 7.01.

Table 3. Example of Shape and Rigidity Factors I for Calculating Settlements of Points on Loaded Area at the Surface of an Elastic Half-Space (from NAVFAC DM 7.01)

As was the case with the stresses in Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads, we use the corners and divide up the entire foundation into four (4) identical foundations. The influence coefficients shown in the DM 7.01 chart above are used. The maximum deflection (at the centre) is thus four times the partial corner deflections.

Here’s where we run into the first problem: the example is wrong because it only considers the corner deflection of one partial foundation. The problem statement implies that, if we add all four partial foundations touching the corners of the partial foundations (which are all at the centre of the full one) we would get the complete settlement at the centre. Doing this yields $\delta_{tot} = 4 \times 0.225 = 0.9'$ .

If we use the Tsytovich chart we can compute the average deflection of the foundation, and we can use the entire foundation at one time. We first note that $\alpha = \frac{l}{b} = \frac{20}{20} = 1$ . We then note that $\frac{h}{b} = \frac{10}{20} = 0.5$ . From the Tsytovich chart $\omega_{mh} = 0.39$ and the settlement as follows:

$\delta_{mh} = 4 \times 20 \times \frac{1-0.5^2}{20} \times 0.39 = 1.17'$ (2)

Although “average” results can be different based on the method of averaging (something students frequently overlook,) it makes sense that a average result should be somewhat below the deflection at the centre. That’s not the case here.

So let’s turn to the newer NAVFAC DM 7.1. They replaced the above chart with the following for settlements:

Figure 1. Elastic Influence Factors for Poisson’s Ratio = 1/2. (a) for mu1, (b) for mu0.

To start with, Figure 5-6 (and the accompanying text) really don’t say whether it’s settlement at the corners, centre or an average settlement. Giroud (1972), the source of Figure 5-6a, does say that it is a corner settlement similar in concept to the old DM 7.01, but the new document does not make this clear. From this, H/B = 10/10 = 1 and L/B = 1. Looking at the chart $\mu_1 = 0.35$ and summing the corner displacements of the partial foundations,

$\rho = 4 \times 1 \times 0.35 \times \frac {4 \times 10}{20} = 2.8'$ (3)

This is significantly different than the old DM 7.01. It is larger than the average settlement shown in the Tsytovich table. But can it be checked against another method?

The answer is “yes,” and to do so we turn to Das (2007). Let us begin by defining the reduced foundation dimensions as B’ and L’, which are obviously half each of B and L. The displacement at the centre of the foundation (the corners of the reduced foundations added together) is thus

$\delta_v = NqB' \frac {1-nu_s^2}{E_s} I_s I_f$ (4)

In this case there are two influence factors, and they correspond with those given in NAVFAC DM 7.1 Figure 5-6: $I_s$ with $\mu_1$ and $I_f$ with $\mu_0$ . We can dispense with the latter by noting that, for the case with no embedment ( $D_f = 0 ,\,I_f = 1$ in a similar way to $\mu_0$ above. (Das gives charts, which we do not reproduce here.) Let us then define

$m = \frac{L'}{B'}$ (5)

and

$n = \frac{H}{B'}$ (6)

Using these ratios, we can define two quantities

$F_1 = \left(m\ln ({\frac {\left (1+\sqrt {{m}^{2}+1}\right )\sqrt {{m}^{2}+{n}^{2}}}{m\left (1+\sqrt {{m}^{2}+{n}^{2}+1}\right )}})+\ln ({\frac {\left (m+\sqrt {{m}^{2}+1}\right )\sqrt {1+{n}^{2}}}{m+\sqrt {{m}^{2}+{n}^{2}+1}}})\right){\pi }^{-1}$ (7)

$F_2 = 1/2\,n\arctan({\frac {m}{n\sqrt {{m}^{2}+{n}^{2}+1}}}){\pi }^{-1}$ (8)

From these quantities,

$I_s = F_1 + \frac{2-\nu}{1-\nu}F_2$ (9)

For our example m = 10/10 = 1 and n = 10/10 = 1. For $\nu = 0.5$ (problem statement,) substituting and solving into Equations (4-8) yields the following:

$F_1 = 0.142$
$F_2 = 0.083$
$I_s = 0.392$

Substituting this yields 2.352′, which is reasonably close to the NAVFAC DM 7.1 solution, and still greater than the solution from Tsytovich.

Notes

The NAVFAC DM 7.1 solution is restricted to values of $\nu = 0.5 $. This is unreasonable; this assumes that the soil is a fluid. It also created a singularity in The Equivalent Thickness Method for Estimating Elastic Settlements.
This shows that even with as venerable a document as NAVFAC DM 7.01 errors can arise, and this should be considered with any book or paper. It also shows that, even with a “cut and dried” topic like theory of elasticity, variations can arise.
All of these solutions are shown in our Elastic Solutions Spreadsheet.
The charts in Das for $I_f = \mu_0$ are similar to the second chart in Figure 1, except that they vary for Poisson’s Ratio and the aspect ratio for the foundation.

References

Das, B.M. (2007) Principles of Foundation Engineering. Sixth Edition. Toronto, Ontario: Thompson.
Giroud, J.-P. 1972. “Settlement of Rectangular Foundation on Soil Layer.” Journal of the Soil Mechanics and Foundations Division, 98(SM1), 149-154.

Academic Issues

The University of Tennessee at Chattanooga College of Engineering and Computer Science is Looking For a New Dean

Posted on 14 February 2023 by Don Warrington

Just a quick note to everyone that the institution I’ve taught at since 2001 is looking for a new Dean. If you’re interested, some links here:

Description of the Role of the Dean of the College of Engineering and Computer Science
Page at Parker Executive Search to submit application. Using a search firm is standard practice at UTC for Dean and higher positions. My experience with other academic searches in this state tells me that one reason they do this is to deal with applicants confidentially, something that is tricky to do with Tennessee’s open records laws.

There is one requirement that merits some comment:

A demonstrated record of intentional and successful actions to foster and enhance inclusion, equity, and diversity…

And this:

UTC takes its commitment to inclusion, equity, and diversity seriously. Letters of interest and other application materials should specifically address the candidate’s intentional and systematic initiatives and accomplishments related to that commitment.

The College of Engineering and Computer Science (including the current Dean) has the most ethnically diverse faculty on campus. This is something the administration does little to publicize.

You can link to Parker’s website to submit an application. If you would like to ask me questions about this, you can go to the Contact page to reach me.

Academic Issues, Geotechnical Engineering

The Equivalent Thickness Method for Estimating Elastic Settlements

Posted on 30 December 20222 January 2023 by Don Warrington

In our very popular post Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads we discuss the use of the theory of elasticity (as originally formulated by Boussinesq) to estimate the stresses and settlements under foundations. We start by giving methods of estimating the stresses under various configurations of rectangular foundations (the circular ones are discussed in the post Going Around in Circles for Rigid and Flexible Foundations.) We then show the use of superposition to expand the use of these results for complex foundations (with further discussion in our post Superposition, and Using Point Loads in Place of Distributed Ones.) We then show the estimation of deflections for simple rigid and flexible foundations. But when it comes to deflections for more complex situations…crickets.

This post is an attempt to solve the “crickets” problem through the use of a method shown in Tsytovich (1976). It’s doubtless useful for preliminary calculations and to enhance our understanding of how settlements of foundations in one place can affect adjacent structures. It also uses some of the linkage between elastic and consolidation settlement theory which is discussed in From Elasticity to Consolidation Settlement: Resolving the Issue of Jean-Louis Briaud’s “Pet Peeve”.

Let us start with Equation (4) of the last linked post, namely

$\epsilon_{{x}}={\frac {p\beta}{E}}$ (1)

where we swap p for $\sigma_x$ as the vertical pressure.

Now let us define an equivalent height h_eq. Keep in mind that we are assuming that the soil’s reaction to vertical pressure is that of a laterally confined specimen; the equivalent height is the height of that equivalent specimen. Multiplying both sides of Equation (1) by this equivalent height,

$h_{{{\it eq}}}\epsilon_{{x}}={\frac {h_{{{\it eq}}}p\beta}{E}}$ (2)

Since by definition

$\epsilon_x = {\frac {s}{h_{{{\it eq}}}}}$ (3)

where s is the settlement, Equation (1) becomes

$s={\frac {h_{{{\it eq}}}p\beta}{E}}$ (4)

Equation (7) of the last linked post tells us that

$E={\frac {\beta}{m_{{v}}}}$ (5)

where

$\beta = 1-2\,{\frac {{\nu}^{2}}{1-\nu}}$ (7)

Combining Equations (4) and (5) yields

$s=h_{{{\it eq}}}pm_{{v}}$ (8)

To compute the equivalent height, we turn to our post Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads, where we modify the equation presented for the deflection of rectangles and squares with Equation (5) above to obtain

$s={\frac {\omega\,pb\left (1-{\nu}^{2}\right )m_{{v}}}{\beta}}$ (9)

The value of $\omega$ is discussed in that post for squares and rectangles and for circles in Going Around in Circles for Rigid and Flexible Foundations. These are very complex (and in the case of circles have no closed form solution.) For convenience the table for these is reproduced below.

If we equate the right hand sides of Equations (8) and (9) and solve for h_eq, we have at last

$h_{eq} = {\frac {\omega\,b\left (1-{\nu}^{2}\right )}{\beta}}$ (10a)

We can also substitute Equation (7) into Equation (10a) and obtain

$h_{eq} = {\frac {\left (-1+\nu\right )^{2}b\omega}{1-2\,\nu}}$ (10b)

If we define

$A = {\frac {\left (1-\nu\right )^{2}}{1-2\,\nu}}$ (10*)

we can also write the equation thus

$h_{eq} = A\omega b$ (10c)

It should be evident that there are several computational routes to obtain the equivalent height, which is then substituted into Equation (8) to obtain the settlement. Let us consider these options:

We could tabulate values of $A \omega$ for various foundation configurations and then use these to compute the equivalent height using Equation (10c). This is given in Tsytovich (1976).
We could determine values for $A$ (it is simply a function of Poisson’s Ratio $\nu$ ), obtain $\omega$ using the table above and then compute the equivalent height using the width of the foundation $b$ . Values for both $A$ and $\beta$ are shown in graphical form as a check for computations.
We could perform direct substitution into Equations (10a) or (10b.) Equation (10a) is probably the best as it will be necessary to compute $\beta$ using Equation (7).

Parameters for Tsytovich Equivalent Thickness Method as a function of Poisson’s Ratio. The red line is the parameter “A” and the green line is the parameter “β”.

Worked Example

As an example, let us consider the same example from the post Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads. The foundation diagram is shown below; we are interested in the settlement at Point A.

The complete solution is given in the same spreadsheet as the solution for the stress problem, which you can access here. The geometry is the same and the loading is the same: 5 kPa on the yellow (2 m x 10 m foundation) and 15 kPa on the brown foundation (2 m x 6 m.) Keep in mind that, for this method, the value b is always the smaller of the two, and that goes for the “void” foundations as well.

We do not need the depth from the surface; we are only interested in surface deflections. We do need the elastic modulus and Poisson’s Ratio of the soil, which are E = 10,000 kPa and ν = 0.25.

The superposition is exactly the same as before, using the following diagram as before:

The superposition scheme is as follows:

Yellow Foundation Positive, corners ABFG, pressure +5 kPa
Yellow Foundation Negative, corners ABJH, pressure – 5kPa
Brown Foundation Positive, corners ACEG, pressure +15 kPa
Brown Foundation Negative, corners ABFG, pressure – 15 kPa

We will only go through the calculations for the first one; you can view the spreadsheet for the rest. We proceed as follows:

We compute A and β as follows:
- From Equation (10*), A = (1-0.25)²/(1-(2)(0.25)) = 1.125
- From Equation (7), β = 1-(2)(0.25)²/(1-0.25) = 0.833
- You can verify these using the plot of these parameters.
We compute the coefficient of volume compressibility by using Equation (5), m_v = 0.833/10000 = 0.0000833 1/kPa
We compute the value of α = l/b = 10/6 = 1.6667
We compute the corner value for ω (since we are dealing with corners as was the case with stresses.) We can use the table for ω or we can compute it using the formulae from Analytical Boussinesq Solutions for Strip, Square and Rectangular Loads, but it is ω = 0.71.
We then use Equation (10c) to compute the equivalent height, thus h_eq = (1.125)(0.71)(6) = 4.8 m. This value will be different for each corner point considered.
Using Equation (8), the settlement for this portion of the analysis is s = (4.8)(5)(0.000083333) = 0.002 m = 1.998 mm.

You repeat this process for all four “foundations.” Keep in mind that the negative foundations will result in negative settlements. A summary of the results is as follows:

Yellow Foundation
Rectangle	B, m	L, m	alpha	omega (corner)	heq, m	Pressure p, kPa	Deflection, mm
ABFG (+)	6	10	1.6667	0.71	4.80	5.00	1.998
ABJH (-)	4	10	2.5000	0.83	3.76	-5.00	-1.565
						Total	0.433
Brown Foundation
Rectangle	B, m	L, m	alpha	omega (corner)	heq, m	Pressure p, kPa	Deflection, mm
ACEG (+)	6	12	2.0000	0.77	5.17	15.00	6.462
ABFG (-)	6	10	1.6667	0.71	4.80	-15.00	-5.994
						Total	0.468
						Complete Total	0.901

Deep Foundations, Pile Driving Equipment

About that “Warrington Method” For Vibratory Pile Drivability — vulcanhammer.info

Posted on 29 December 202227 December 2022 by Don Warrington

Every now and then something comes up that you really didn’t expect. That took place with a paper published this year cited “W.J. Lu, B. Li, J.F. Hou, X.W. Xu, H.F. Zou, L.M. Zhang, “Drivability of large diameter steel cylinders during hammer-group vibratory installation for the hong kong–zhuhai–macao bridge,” Engineering (2022), doi: https://doi.org/10.1016/j.eng.2021.07.028.” (You can […]
About that “Warrington Method” For Vibratory Pile Drivability — vulcanhammer.info

	Fraction of Pressure			Soil Vertical Reaction, ksf
$\xi$	Rigid Foundation	$\Gamma = 3$	Flexible Foundation	Rigid Foundation	$\Gamma = 3$	Flexible Foundation
0.0625	0.828	0.876	1	3.312	3.504	4
0.1875	0.829	0.874	1	3.316	3.496	4
0.3125	0.836	0.874	1	3.344	3.496	4
0.4375	0.837	0.866	1	3.348	3.464	4
0.5625	0.857	0.87	1	3.428	3.48	4
0.6875	0.899	0.893	1	3.596	3.572	4
0.8125	0.987	0.958	1	3.948	3.832	4
0.9375	1.927	1.791	1	7.708	7.164	4

Some Review: Purely Rigid Foundations

Non-Infinite Spaces and Flexible Foundations

Non-Infinite Spaces and Rigid Foundations

Foundation Flexibility

Other Representations of Relative Rigidity

Share this:

Notes

Share this:

Share this:

Worked Example

Share this:

Share this: