Academic Issues – Page 4 – vulcanhammer.net

A Simplified Method to Design Cantilever Gravity Walls

Posted on 6 October 202316 June 2025 by Don Warrington

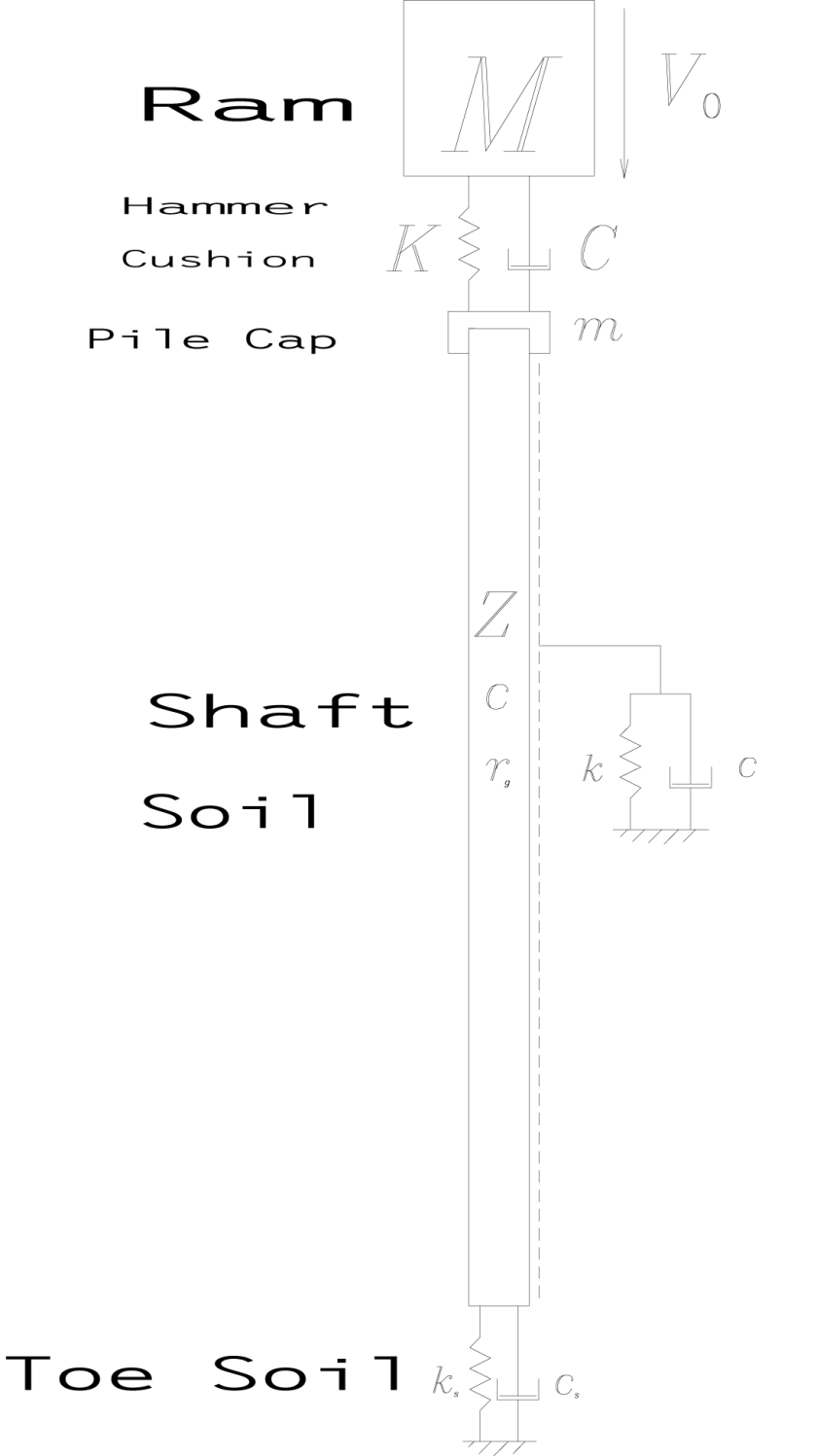
On this site we feature the U.S. Army Corps of Engineers publication Retaining and Flood Walls, which details the design of several types of retaining walls. As it was published a good while back, it details the design of these walls using hand calculations. Sometimes these can get tedious, especially when the aptly named “trial wedge” solutions are employed.

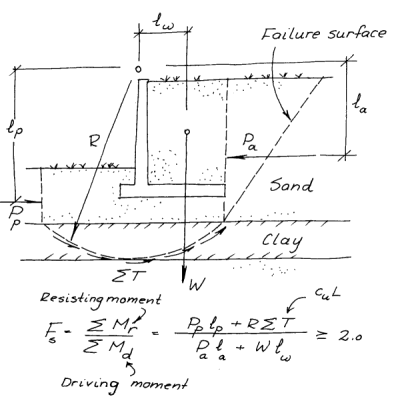
These days it’s more likely that a computer solution–be it a true finite element analysis or simply the automation of those tedious hand calculations–is used to finalise the design of a retaining wall. An example of such an analysis is shown above, and addresses in particular an issue that gets the short shrift in classical retaining wall analysis of any kind: global stability failure. An idea of a hand solution to this problem is shown at the right. Global stability failures still happen and are generally disastrous; beyond a conventional slope their analysis is fairly complex.

But in the meanwhile, what do we do to verify that we’ve got it right with a computer solution? Or what can we do to start with a reasonable design that we can refine with numerical analysis? Back in the “slide rule era” we used quick, “back of the envelope” methods to design things, and we can use them today both to get started and to gain a basic understanding of the elements of the design.

In this case we’re going to discuss the design of a cantilever retaining wall, an example of which is shown below.

The methodology is based on the aforementioned Retaining and Flood Walls and the example (which is a little clearer description of same) comes from Appendix A of Seismic Analysis of Cantilever Retaining Walls, Phase I. I’ve modified it in a couple of spots and will detail those modifications as we go.

The example we’ll look at is below. We need to design this wall to prevent failure against three events: sliding, overturning and bearing capacity failure.

Defining the Geometry, Weights and Centres of Gravity

Our datum/coordinate origin is at the toe, which is convenient since we assume that the overturning moment is computed around the toe. Since this is a cantilever/gravity wall, the weight of the wall is part of the resistance force and moment. Included with that is the backfill that is trapped behind the wall (shown above.)

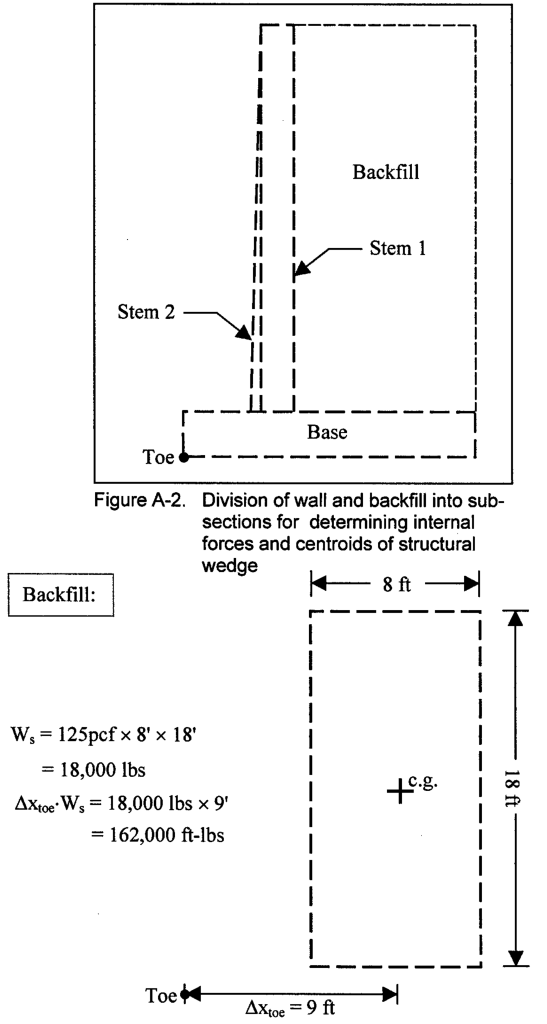
We start by dividing up the wall into sections, each of which has a weight and a centre of gravity. The first section we take up is the backfill, which is a simple rectangle shown above.

At this point we need to make one correction to the Corps’ work: the weights and moments are in pounds per unit length of wall and ft-pounds per unit length of wall, respectively. Leaving those per unit length designations is a common shortcut among practitioners but is confusing for students, who frequently find the unit length concept difficult to grasp at first. The weight of the backfill is properly 18,000 lbs/ft of wall and the moment around the toe ((clockwise) is 162,000 ft-lbs/ft of wall.

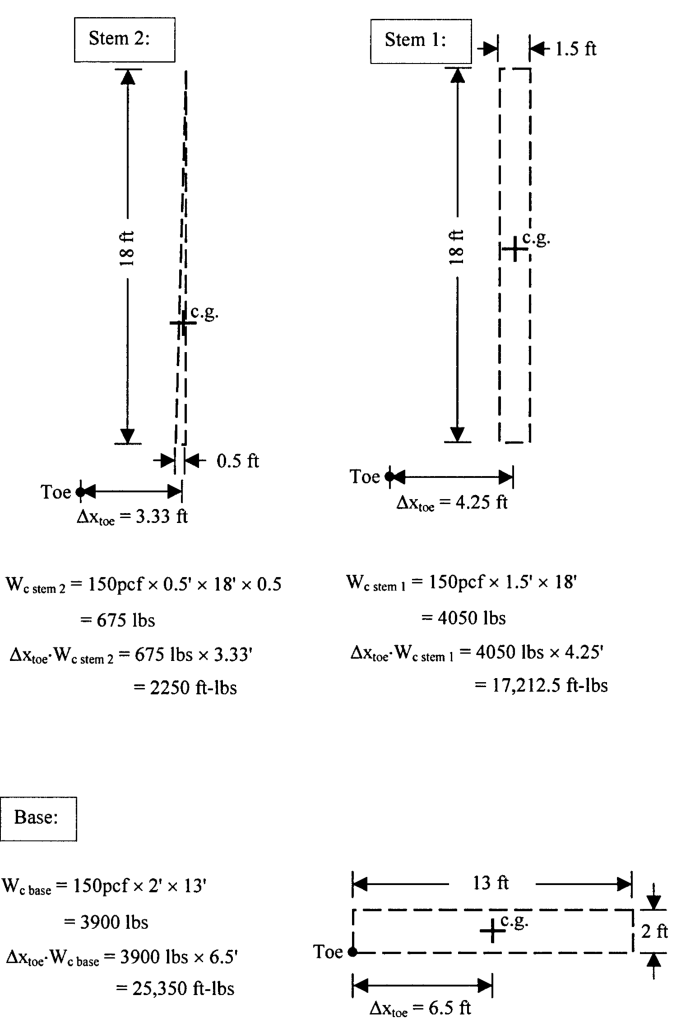
Computing the weights and moments of the various sections of the wall itself yields the following results.

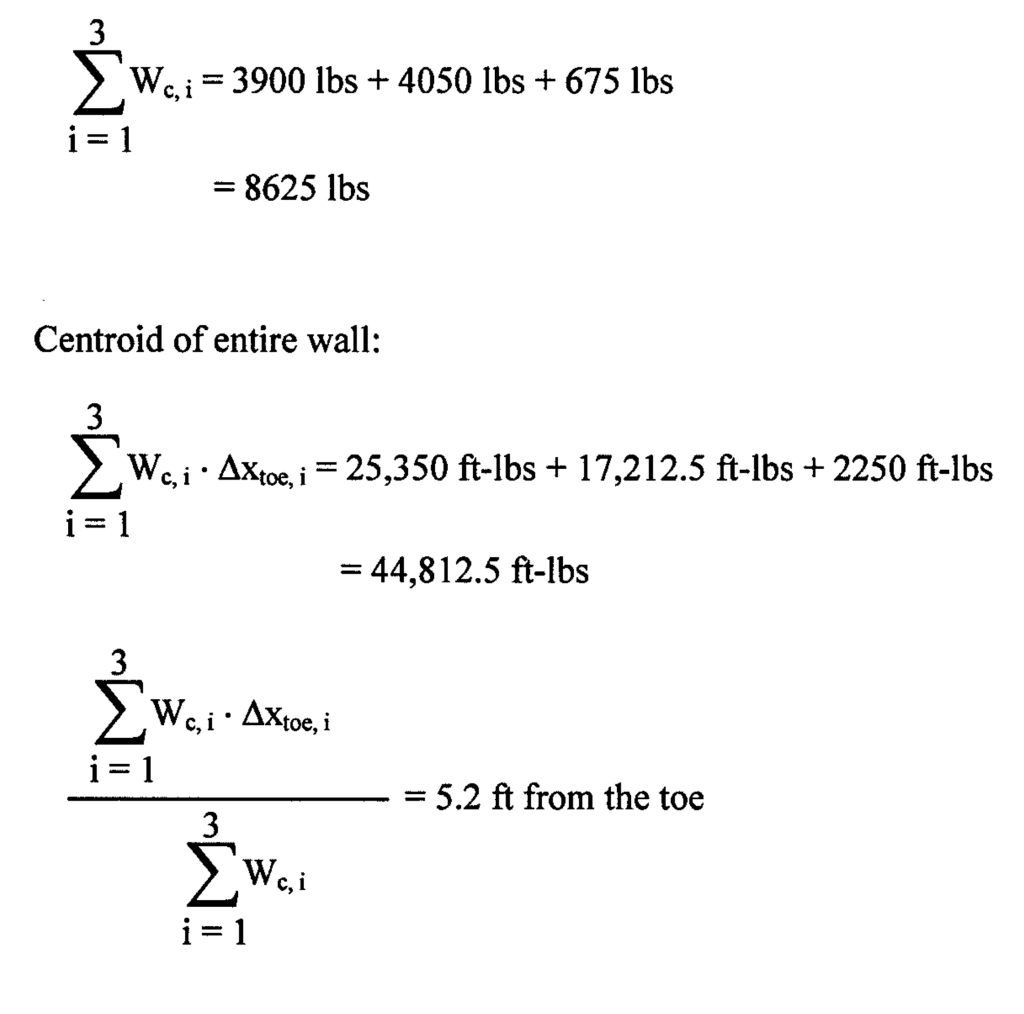
Taking all of this information and processing it yields the total weight, total moment around the toe, and moment arm around the toe:

Since most engineers have learned their statics via vectors, a review of Vector Statics and “Old Coot” Statics: An Example and What is a Resultant in Geotechnical Engineering? may be in order.

The Shear Mobilisation Factor

Now comes the tricky part: in retaining wall design, we traditionally define the factor of safety as

$FS = \frac{F_{resisting}}{F_{driving}}$ (1)

Where the “F” values can be forces or moments and FS is the factor of safety. Sometimes this is not the optimal way of applying factors to account for uncertainties, especially when we get to LRFD. Another approach is either to increase the driving force or reduce the resisting force. We do the latter with sheet piling (where there there are earth forces to resist) but here we’ll to the former. To make this happen we first define a shear mobilisation factor (SMF) thus

$SMF = \frac{\tan \phi'_{mob}}{\tan \phi'}$ (2)

The value of $\phi'_{mob}$ can be computed thus:

$\phi'_{mob} = \tan^{-1}(SMF tan \phi')$ (3)

For this problem, assuming SMF = 2/3 and φ’ = 35°, by substitution φ’_mob = 25°. We will discuss the effect of cohesion later.

Now we turn to computing the force of the soil behind the wall on the wall.

We note the following:

Rankine theory is used. Methods shown in both Retaining and Flood Walls and the Soils and Foundations Reference Manual use Coulomb and/or log-spiral for these computations. The problem with this is that the value of wall friction δ is sometimes difficult to determine without data or experience, and in reality most of this pressure bears on soil, not the wall. So Rankine is easier to start with, and is more conservative.
The backfill is level, the formula for Ka only applies in that case. We will discuss sloping backfill below.
Note that φ’_mob (not φ’ ) is being used to compute the soil force.

Analysing Sliding and the Location of the Resultant/Overturning

At this point we can compute the forces on the base (both the forces T’ and N’ and the location of the resultant x_N’,) which are shown below.

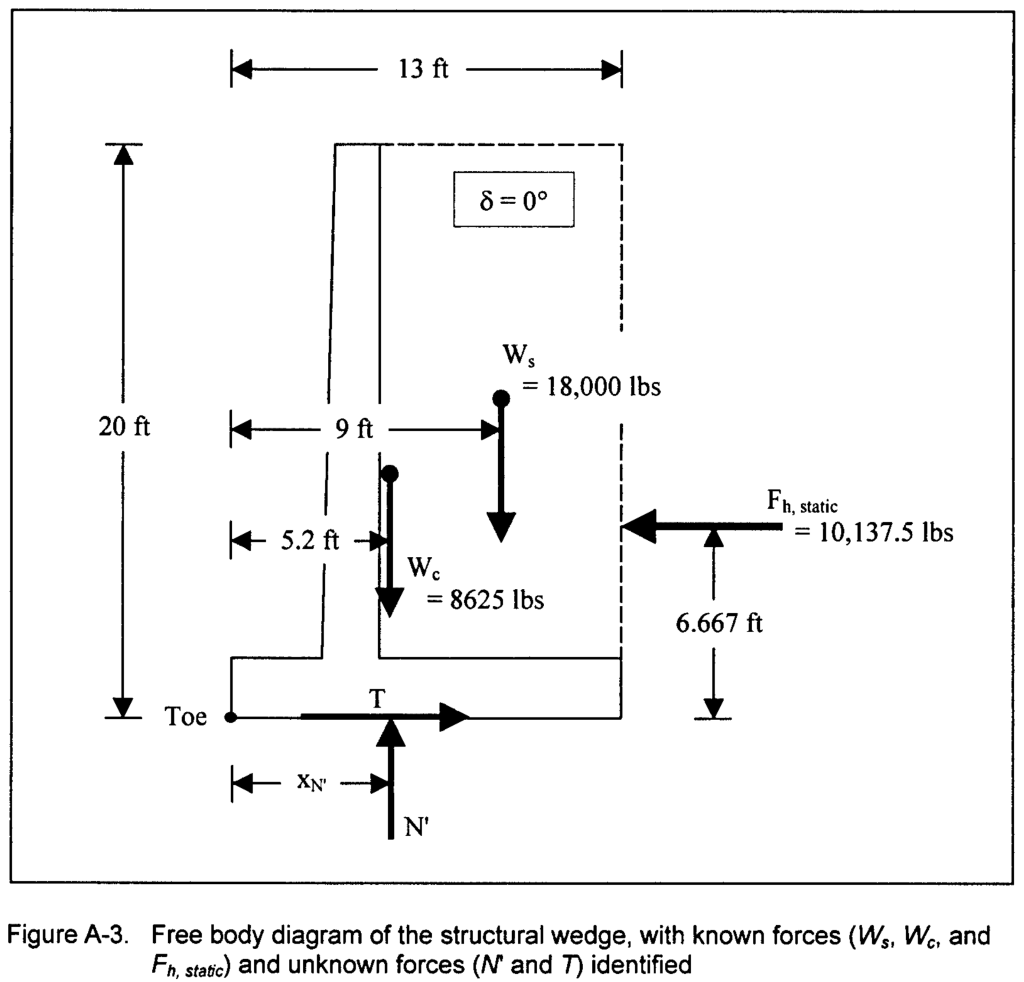
The calculations are shown below.

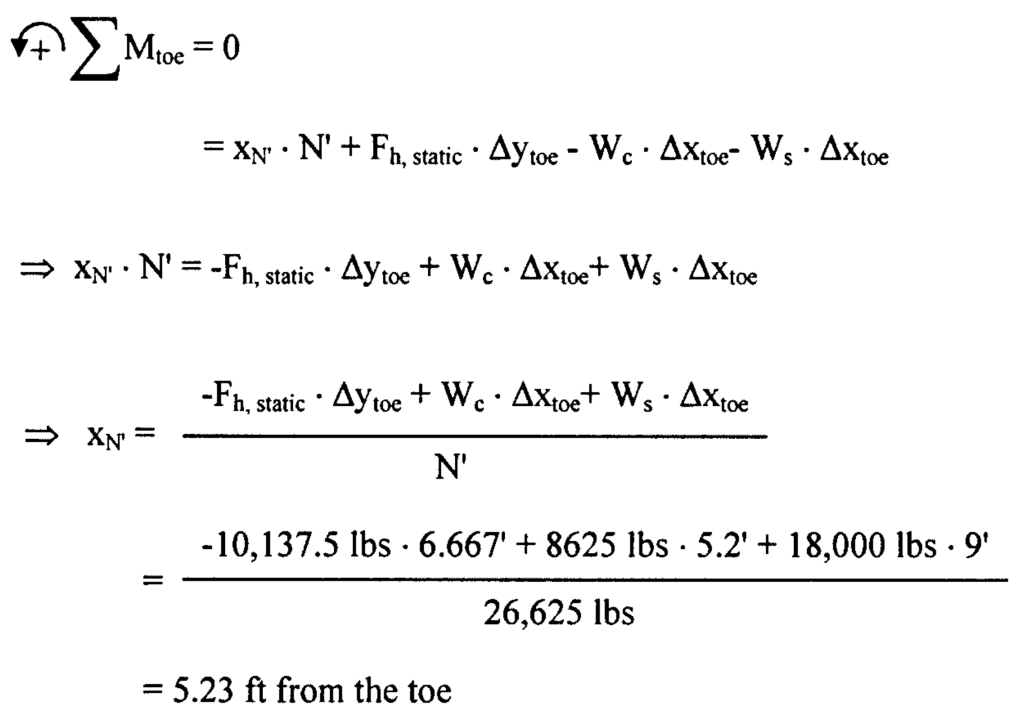
Turning to the sliding problem, the driving force is the earth pressure force and the resisting force is the maximum Coulomb friction of the base/soil interface. In this case the value of δ is equated to the unmodified value of φ’, although that isn’t always the case. (The basis for this is that there is a thin layer of backfill sand under the wall, under which is a different foundation soil.) We then apply Equation (1) and determine the factor of safety against sliding, which checks out against the Corps criteria.

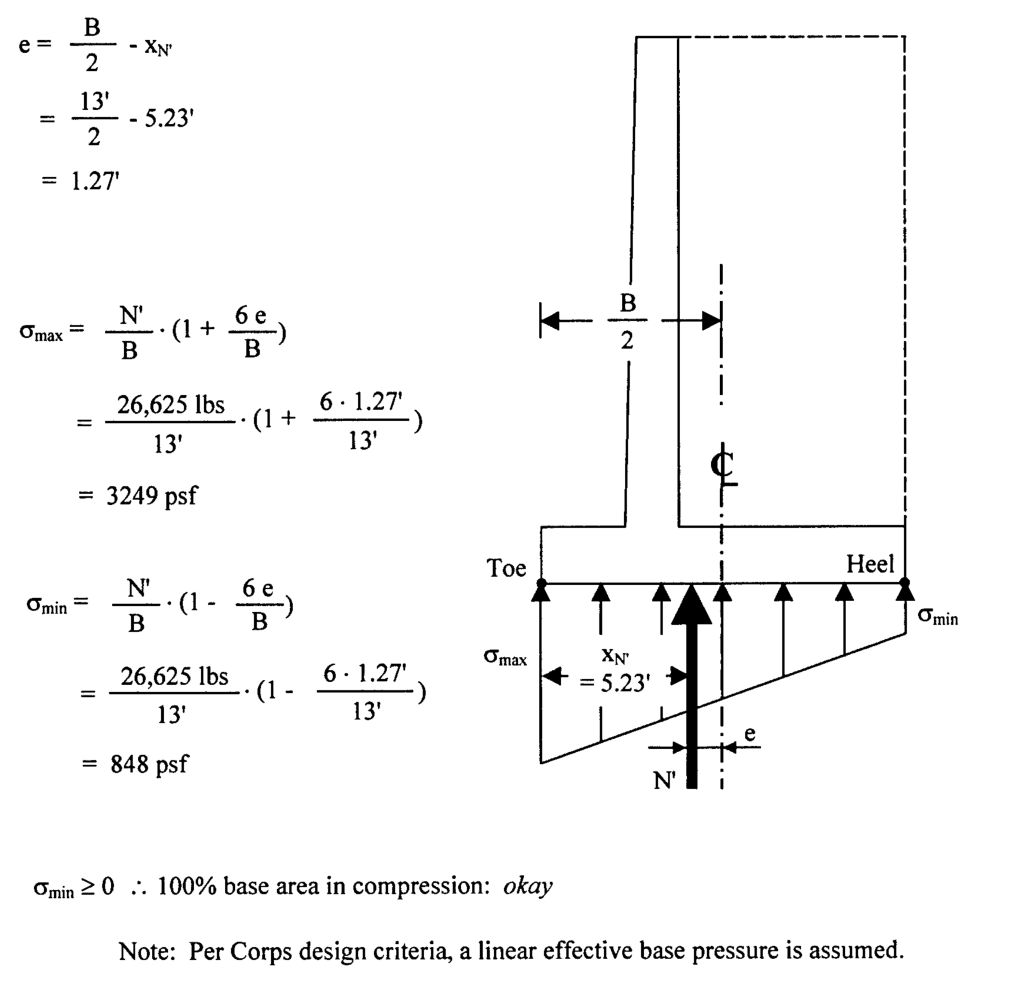
Knowing the location and magnitude of the resultant, we compute the maximum and minimum pressures on the base. Since both pressures are compressive, the resultant is in the middle third, and thus we can proceed with the base design.

One thing that is missing from this analysis is a specific analysis for overturning. In this case we make a common assumption that, as long as the resultant force of the wall is within the kern and there are no negative pressures on the base, overturning will not be experienced. It is certainly possible to do an explicit overturning analysis to check this result.

Bearing Capacity Analysis

With the wall’s sliding and overturning established, we turn to the bearing capacity analysis of the base. The complete bearing capacity equation, from the Soils and Foundations Reference Manual (with modification,) is

$q_{ult}=s_{c}b_{c}l_{c}cN_{c}+s_{q}b_{q}l_{q}C_{wq}q_{o}N_{q}+\frac{1}{2}s_{\gamma}b_{\gamma}l_{\gamma}C_{w\gamma}\gamma B_{f}N_{\gamma}$ (4)

where

q_ult = ultimate unit upper bound bearing capacity
s_c, s_γ and s_q = shape correction factors. These are unity in this case since it is a continuous foundation (generally the case with retaining walls)
b_c , b_γ and b_q = base inclination correction factors (unity in this case since the foundation is level)
C_wγ and C_wq are groundwater correction factors (unity in this case since groundwater isn’t an issue, a rare event with retaining and especially flood walls)
I_c, I_γ and I_q = load inclination factors, discussed below
N_c , N_q and N_γ are bearing capacity factors that are a function of the friction angle of the soil. N_c , N_q and N_γ are shown in the table below. These are handled differently when a slope is present. They are given in the Soils and Foundations Reference Manual. There is a general consensus for N_c and N_q but not N_γ. In this case we will use Vesić’s values for it, following AASHTO/FHWA practice. For this case the base soil φ’ = 40° we have N_c = 75.3, N_q = 64.2 and N_γ = 109.4
B_f = Base width of the foundation. In this case, with an eccentrically loaded foundation, this must be reduced to the equivalent foundation width by the formula B’_f = B_f – 2e = 13 – (2)(1.27) = 10.46’.
q₀ = overburden pressure on the base from the dredge (low) side of the wall. For walls such as this we neglect all effects of this, both any potential passive lateral pressure and overburden pressure.
c = cohesion of the soil = 0
- Because of this and the previous point, we can neglect the first two terms of Equation (4) and only concern ourselves with the last one.

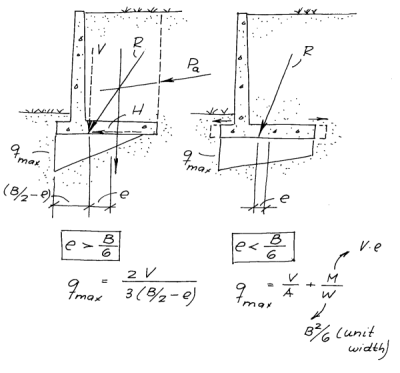
Load inclination is the result of two perpendicular loads acting on the base of the foundation. It is illustrated in the sketch at the left.

The load inclination factors are given as follows:

$l_{c}=l_{q}=\left(1-\frac{\delta'}{90\textdegree}\right)^{2}$ (5a)

$l_{\gamma}=\left(1-\frac{\delta'}{\phi'}\right)^{2}$ (5b)

where the load inclination angle is given as follows

$\delta' = \tan^{-1}\frac{T}{N'}$ (6)

Substituting yields 𝞭’ = tan^-1 (10,137.5 lbs/26,625 lbs) = 20.8°. The friction angle of the base soil proper is 𝟇 = 40°. Substituting into Equation (5b) yields l_𝞬 = (1-20.8/40)² = 0.23. We can neglect the factors for Equation (5a) as those terms do not apply to this situation, but for completeness l_c = l_q = (1-20.8/90)² = 0.591.

Making all relevant substitutions:

q_ult = (0.5)(1)(1)(0.23)(1)(10.46)(125)(109.4) = 16,450 psf
Q_ult = q_ult B_f = (16,450)(10.46) = 172,067 lbs. = 172 kips
N = 26,625 lbs
FS = Q_ult/N = 172067/26625 = 6.46 (acceptable)

Settlement Analysis

Settlement of retaining wall is an important topic, as settlement of walls and levees has led to overtopping (as we found out the hard way during Hurricane Katrina.) Instead of picking a method and doing it “by hand,” we will use the USACOE software package CSANDSET, developed by Virginia Knowles. To accomplish this we need to do the following:

The foundation with we use is the reduced foundation width, or B’_f = B_f – 2e = 13 – (2)(1.27) = 10.46’.
The normal load is N = 26,625 lbs.
The unit load on the foundation is thus 26625/(2000*10.46)=1.27 tsf (the units used by the program.)
We assume a length of 50′; this puts the L/B > 10, which is an assumption for continuous foundations.

The input data is shown in the screenshot below.

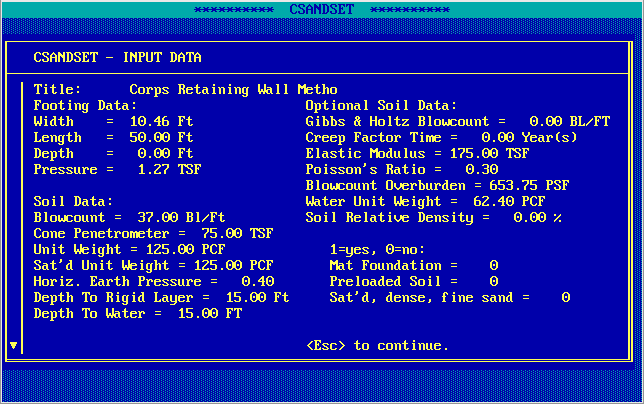
The SPT and CPT are taken from “typical” values as they were not given in the problem statement. The option data is generated by the program. The horizontal (at-rest) earth pressure is Jaky’s Equation for normally consolidated soils.

The solutions the program gives are as follows:

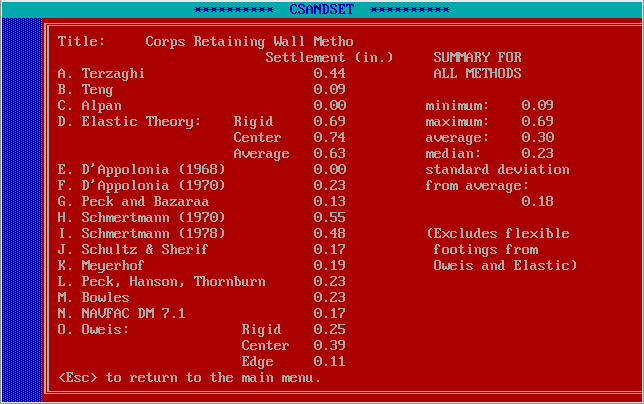
The various methods are described in the program documentation. Schmertmann’s Method is given a full description in Foundation Design and Analysis: Shallow Foundations, Settlement. Elastic methods are treated in Soil Mechanics: Elastic Solutions to Soil Deflections and Stresses and related posts. It is interesting to note the wide variance in results; this is typical of geotechnical methods in a state of flux, and can also be applied to bearing capacity of driven piles.

The supplemental data generated by the program is at the end of the post.

Dealing with Sloping Backfill

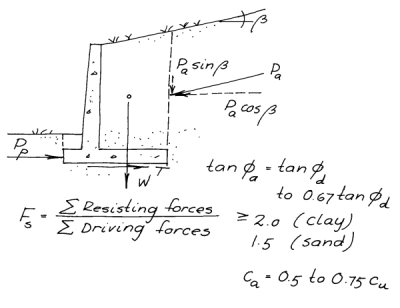
The example problem above has a level backfill. Sloping backfills–usually positive (up from the wall,) occasionally negative, are common with retaining walls. The problem of the sloping backfill is illustrated at the right.

Without going into the actual solution of the problem using a sloping backfill, the following changes must be made in order to accommodate the effects of this condition:

The Rankine equation for sloping backfill needs to be applied. This can be found in the post Rankine and Coulomb Earth Pressure Coefficients. The coefficient computed is actually Coulomb theory applied without wall friction; the differences between this and “extended Rankine” theory for sloping backfill are discussed in the post on the coefficients.
An additional region needs to be defined with the soil below the sloping backfill (assuming it’s positive) as shown in the diagram below.
The length a of this region is already defined. The length b is given by the equation b = a tan (β). That length is important in a) computing the weight of the region and b) computing the additional length of the height the soil bears on the wall, or H + b.
The backfill force must be separated into horizontal and vertical components, as shown in the diagram above. The vertical component actually increases both the weight on the foundation and the resisting moment of the weight.

Assuming a β = 10° and applying φ’_mob = 25°, with the geometry shown we note the following:

With the two angles shown, K_a = 0.462, which is higher than the level backfill value.
The value of b = (8)(tan(10°))=1.41′. This means that the total height is 20 + 1.41 = 21.41′.
The lateral pressure at the base is (0.462)(21.41)(125) = 1236.5 psf.
The total lateral force on the wall F_h is (1236.4)(21.41)/2 = 13,236 lb/ft of wall. The resultant of that force is 21.41/3 = 7.14′ above the base of the foundation.
That lateral force has a horizontal component of (13236)(cos((10°)) = 13,035 lb/ft and a vertical component of (13236)(sin(10°)) = 2298 lb/ft. The latter has a moment arm of 13′ from the toe.
The area added by the sloping backfill has a weight W_ba = (125)(8)(1.41)/2 = 705 lb/ft. Its centroid is located 5 + (2)(8)/3 = 10.3′ from the toe.

We will leave working out the effects of this backfill slope to the reader.

The Shear Mobilisation Factor (SMF) and Cohesive Soils

If we have soils with cohesion in the backfill, the cohesion should be modified in a similar way to the friction angle thus:

$c' = c \times SMF$ (7)

A more complete treatment of the SMF is given in Retaining and Flood Walls.

Academic Issues

My View of Student Evaluations

Posted on 21 September 2023 by Don Warrington

One thing any academic does (except those at grand institutions where they get to have someone else do it for them) is evaluate students through grading. Most institutions afford students the opportunity to retaliate through the faculty evaluation system in place. That usually takes places at the end of the term, although my institution now had mid-term evaluations in place.

Student evaluations of faculty always take me back to this incident in my own undergraduate saga:

One of the things that the Mechanical Engineering department required* its majors to take was Logic, which was offered by the Philosophy Department. Most of the engineers did pretty well in this course, which was doubtless a source of secret frustration to liberal arts’ professors.

One day I went up to pick up a test from the professor. The professor looked at the grade, noted that I had nearly aced it, looked at me, and exclaimed, “You’re not as dumb as you look!”

The purpose of student evaluations of me is to determine whether they agree with my Logic teacher’s opinion or not.

*Originally posted here. Since then I discovered that there was another option available, but my advisor at the time did not avail me of that choice.

Academic Issues, Deep Foundations

Comments on “Using the Impulse–Response Pile Data for Soil Characterization”

Posted on 5 August 20235 August 2023 by Don Warrington

It’s citation time again; this paper, authored by Heeyong Huh, Heedong Goh, Jun Won Kang, Stijn François and Loukas F. Kallivokas, cites both Closed Form Solution of the Wave Equation for Piles and Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles. It is available here. The abstract is as follows:

The impulse–response (IR) test is the most commonly used field procedure for assessing the structural integrity of piles embedded in soil. The IR test uses the response of the pile to waves induced by an impulse load applied at the pile head in order to assess the condition of the pile. However, due to the contact between the pile and the soil, the recorded response at the pile head carries information not only about the pile, but about the soil as well, thus creating the as-yet-unexplored opportunity to characterize the properties of the surrounding soil. In effect, such dual use of the IR test data renders piles into probes for characterizing the near-surface soil deposits and/or soil erosion along the pile–soil interface. In this article, we discuss a systematic full-waveform-based inversion methodology that allows imaging of the soil surrounding a pile using conventional IR test data. We adopt a heterogeneous Winkler model to account for the effect of the soil on the pile’s response, and the pile’s end is assumed to be elastically supported, thus also accounting for the underlying soil. We appeal to a partial differential equation (PDE)-constrained-optimization approach, where we seek to minimize the misfit between the recorded time-domain response at the pile head (the IR data), and the response due to trial distributions of the spatially varying soil stiffness, subject to the coupled pile–soil wave propagation physics. We report numerical experiments involving layered soil profiles for piles founded on either soft or stiff soil, where the inversion methodology successfully characterizes the soil.

Over the years I have been looking at many different aspects of the problem of pile dynamics, which includes both prediction of drivability of piles and the inverse problem of estimating the static resistance of piles based on their performance during driving. In the course of working with all of this many ideas have come to mind; two of those are as follows:

Is it possible to use the model (or something like it) in Closed Form Solution of the Wave Equation for Piles for the inverse method? My experience with Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles and its progeny informed me that managing the inverse method in a full FEA model including pile and soil was difficult and getting past uniqueness issues (which have plagued pile dynamics from the start) was next to impossible.
Is it possible to use the pile hammer as a geotechnical sounding tool to determine the properties of soil layers into which the pile is being driven? In Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles the soil at any given point was defined by the “Mohr-Coulomb triple” (unit weight, internal friction angle and cohesion) along with other properties, which is the point for most soil testing. The inverse method returned those properties.

The present paper does some interesting things to get to those solutions but ultimately doesn’t quite get to reaching a solution to these problems.

The Strong Point

Probably the strongest point of the paper is the entire mathematical presentation, from the development of the method to its execution. It shows computational proficiency of a high order. For example, it is the first time in pile dynamics that I have seen the use of the conjugate gradient technique. As the product of a PhD program with a heavy emphasis on computational fluid mechanics, this technique was well familiar to me (along with GMRES, which was the method of choice for my colleagues.) One of the challenges the geotechnical industry faces moving forward is the proper application of numerical techniques to geotechnical problems which are non-linear in ways which are unknown in other fields. We have people who are specialists with the geomechanics and people who are specialists in numerical methods, but few are those who are proficient in both.

One thing I would like to mention is that my use of a polytope method–which had many drawbacks–was driven by the difficulties in optimising geotechnical problems. Those difficulties are caused largely by the existence of false minima and maxima in the solution. It is why we still see, for example, grid optimisation used for slope stability problems: the use of, say a Newton’s Method type of optimisation may easily result in finding a false minimum. Although I think the author’s techniques have great promise of solving these problems, it is something they will have to watch for moving forward.

The Soil Property Issue

Probably the greatest weakness of the paper is the way soil properties are characterised.

Let us first consider the system model presented in Closed Form Solution of the Wave Equation for Piles, shown below.

Simplified Hammer-Pile-Soil System (from Warrington (1997))

In this diagram the ram mass M impacts the cushion with a velocity V_o. There are several stiffnesses and damping coefficients k and c respectively. The accessory has a mass of m. The pile has an acoustic speed c, an impedance Z and a geometry ratio r_g. For inverse analysis the hammer, cushion and driving accessory can be deleted and a force F(t) and velocity V(t) (both a function of time) substituted at the pile head.

The equation of motion u(x,t), which is a function of both the distance from the pile head x and time t, is given by the equation

${c}^{2}{\frac {\partial ^{2}}{\partial {x}^{2}}}u(x,t)={\frac {\partial ^{2}}{\partial {t}^{2}}}u(x,t)+au(x,t)+2\,b{\frac {\partial }{\partial t}}u(x,t)$ (1)

The variables a and b are stiffness and damping related coefficients which are related to k and c by geometric and material property considerations, as discussed in Closed Form Solution of the Wave Equation for Piles.

Although the present paper allows for k(x), the one major difference between the governing equation presented above and the one in the paper is the omission of damping by the latter. (This omission is also repeated at the pile toe.) The soil damping is for the most part a representation of the propagation of wave energy from the pile as it is dynamically loaded. It is impossible to avoid in one form or another. First derivatives like that are always a danger in problems such as this. One way to get around that is to redistribute the damping into the spring and mass terms using Rayleigh damping. This is very frequency dependent and can be tricky to accurately apply; however, if it can be done successfully (and the authors’ note of wavespeed changes with soil interaction may be part of the solution) it would bypass the problems created by the first derivative. (The same comments regarding the shaft also apply at the toe, where an additional mass would have to be applied to achieve Rayleigh damping.)

But that doesn’t address what is, in some ways, the more serious issue: applying a linear model to a very non-linear problem. Concentrating on the shaft resistance, let us begin by noting the results in Estimating Load-Deflection Characteristics for the Shaft Resistance of Piles Using Hyperbolic Strain Softening, and stipulating that, even with hyperbolic stress-strain considerations, up to the time of separation between the shaft and the soil the load-deflection relationship is essentially linear. This study showed that, for the specific case in question, the geometric nonlinearity of the deflecting soil around the shaft and the material nonlinearlity of the soil offset each other to a large degree. Obviously more study needs to be done but this is a start.

Having said that, let us look at a diagram I have used and modified over the years:

At zero strain we have the small strain elastic or shear modulus. As strain increases, if we use a linear model for load-deflection the only way the model can simulate that kind of response is to do some kind of “secant modulus” estimate. What this means is that the elastic modulus/shear modulus/spring constant is strain dependent, which will vary with loading condition (to put it in classical geotechnical terms, to what extent the shaft resistance is mobilised.) It is also worth noting that this mobilisation is not identical in static and dynamic testing, even on the same pile.

Based on all of this, it is difficult to see how the results of the inverse method can be used to accurately characterise the load-deflection characteristics of the pile, let alone the properties of the soil.

I should note that quite a few of my comments in Comments on “Fictitious soil pile model for dynamic analysis of pipe piles under high-strain conditions” apply to this situation as well. This linearity problem is a major reason why I never have attempted to use the model in Closed Form Solution of the Wave Equation for Piles as a “full-up” inverse method.

Conclusion

This paper is an interesting study of the problem at hand. While some significant advances have been done in the numerical treatment of the problem, the physics of the pile-soil system need to be re-examined and improved.

Academic Issues, Deep Foundations

Comments on “Fictitious soil pile model for dynamic analysis of pipe piles under high-strain conditions”

Posted on 3 August 20235 August 2023 by Don Warrington

Once again I find myself cited, this time in this paper by Yuan TU , M.H. El Naggar , Kuihua Wang , Wenbing WU , and Juntao WU. The citation comes from my paper “A New Type of Wave Equation Program,” documenting the development of the ZWAVE computer program. The abstract of this paper is as follows:

A fictitious soil pile (FSP) model is developed to simulate the behavior of pipe piles with soil plugs undergoing high-strain dynamic impact loading. The developed model simulates the base soil with a fictitious hollow pile fully filled with a soil plug extending at a cone angle from the pile toe to the bedrock. The friction on the outside and inside of the pile walls is distinguished using different shaft models, and the propagation of stress waves in the base soil and soil plug is considered. The motions of the pile−soil system are solved by discretizing them into spring-mass model based on the finite difference method. Comparisons of the predictions of the proposed model and conventional numerical models, as well as measurements for pipe piles in field tests subjected to impact loading, validate the accuracy of the proposed model. A parametric analysis is conducted to illustrate the influence of the model parameters on the pile dynamic response. Finally, the effective length of the FSP is proposed to approximate the affected soil zone below the pipe pile toe, and some guidance is provided for the selection of the model parameters.

The topic is an interesting one which I have touched on over the years. It seems to me that their characterisation of the model as “novel” may be a bit of a stretch but their implementation of it is very interesting.

What is a Fictitious Pile Model?

Most of us in the driven pile industry are familiar with the one-dimensional wave equation, which divides up the pile into discrete segments/elements and by doing so models the distributed mass and elasticity (or plasticity) or the system, such as is shown in Figure 1, from the Design and Construction of Driven Pile Foundations, 2016 Edition:

Figure 1 One-Dimensional Wave Equation Method Diagram (from Soils and Foundations Reference Manual)

An advance of this is the use of two- or three-dimensional elements in a finite element scheme, such as was featured in the earlier post Comments on “3D FE analysis of bored pile- pile cap interaction in sandy soils under axial compression- parametric study” and was analysed extensively in my dissertation Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles. A cross section of that model is shown in Figure 2, from Inverse Analysis of Driven Pile Capacity in Sands:

Figure 2. Cross-Section of Finite-Element Model for Pile and Soil (from Warrington (2020))

Note that the pile, which is in red, is basically a one-dimensional string of elements with distributed mass and elasticity. It’s worth noting, however, that using two- (or three- for that matter) dimensional elements enables the element to have a non-uniform stress distribution which would reflect the effect of the soil resistance, but let us set this last point aside.

Such a model as shown above models both the shaft friction along the side of the pile and the toe resistance under the end of the pile. It has been customary over the years, however, for researchers and practitioners alike to model this resistance in a rheological way. This has been easier with the shaft than with the toe, because of the complexities of the dynamic elasto-plastic response of the soil at the toe and the difficulties of establishing failure surfaces in the soil has led to many solutions of the problem.

One of those is to construct a fictitious pile under the toe which, instead of the straight sides we usually (but not always) see with piles, has a conical shape, so as the distance from the toe increases the size of the fictitious pile likewise increases.

Figure 3. Fictitious Pile Model for the Pile Toe (from Holeyman (1988); Warring-
ton (1997))

The first proposal of this came from Holeyman (1988) and was discussed in Closed Form Solution of the Wave Equation for Piles and more recently in the paper STADYN Wave Equation Program 10: Effective Hyperbolic Strain-Softened Shear Modulus for Driven Piles in Clay. A diagram of this is shown in Figure 3. Although the model is generally done (as is the case in the models in Figure 1) with discrete elements, it can be modeled continuously. The paper under consideration did so using finite elements. A problem that occupied this researchers and those of the paper under consideration is the value of H, which does not have an “obvious” solution from the physics of the problem.

In the work under review, in addition to using finite elements the authors made two important improvements to the model shown in Figure 3:

They added a “shaft” resistance along the side of the fictitious piles.
They put a hole in the centre of the fictitious pile to assist in simulating the soil plug, which was one of the main goals of the study. Soil plugging is a difficult phenomenon in open-ended piles, and although we’ve made some progress in modelling it we still have a long way to go.

Some Comments on the Study Itself

The authors used ABAQUS to model both piles. This is a code which has been applied to geotechnical problems for at least thirty years, so it has a long track record. Having started from “scratch” with Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles, I can attest that using a software package saves a great deal of time and effort, in addition to making graphical presentation of the results a good deal simpler. Having said that, if anyone has an ambition to use FEA to replace, say, GRLWEAP or CAPWAP, they’ll have to either a) pay licensing fees to a cut down “engine” from an established package like ABAQUS or b) use an open source alternative.

At the start of the study they make the following statement:

Open-ended pipe piles are increasingly used worldwide as foundations for both land and offshore structures [1,2]; therefore, the characterization of pipe pile capacity and behavior under static and dynamic loading conditions has gained much attention in recent years [3–5].

Open ended pipe piles have been used for much longer that this paragraph would imply, as this whole series will show. Getting them in the ground was much of the impetus for the TTI wave equation program, and the lateral loads they withstood were much of the push behind the development of p-y methods. And that was in the 1960’s and 1970’s.

The soil model they use is a cross between a elastic-purely plastic model and a hyperbolic soil model. Reconciling the two has been a preoccupation of this site since Relating Hyperbolic and Elastic-Plastic Soil Stress-Strain Models: A More Complete Treatment. Although the model they use certainly takes into consideration hyperbolic strain softening, I’m not convinced that their assumption that the rebound runs along the small-strain modulus of elasticity is valid. On the other hand I’m not sure what the best way out of this dilemma is; hyperbolic soil modelling hasn’t been as thorough in analysing the stress-strain characteristics of soil during rebound as it has been in doing so during loading.

One thing I noticed is the variance between the static load test results and that shown in the model. That’s not unexpected; I’ve encountered this difficulty, as you can see from this figure in STADYN Wave Equation Program 10: Effective Hyperbolic Strain-Softened Shear Modulus for Driven Piles in Clay:

On the other hand, it’s possible to get a closer result, as is seen in Application of the STADYN Program to Analyze Piles Driven Into Sand:

The basic problem is twofold:

Although the relationship between the shear modulus of soils and the void ratio or porosity is well established, the coefficient used to determine the former from the latter is subject to uncertainty.
The static and dynamic shear moduli of soils is different, which is an issue in pile dynamics that has not been adequately explored.

Conclusion

The paper is an excellent step forward, and the model presented has a great deal of potential in pile dynamics. It may be easier to use such a model than a full axisymmetric or 3D model to obtain the inverse solution to the problem, but many of the issues discussed here–such as the angle and depth of the fictitious pile cone and the shear moduli of the soils in question–need better resolution.

As far as the plugging issue is concerned, any advance in this is welcome, although I am inclined to think that a model which simulates the full, blow-by-blow installation of the pile with the formation of the plug, will ultimately be the best solution of the problem.

Academic Issues, Deep Foundations

Comments on “3D FE analysis of bored pile- pile cap interaction in sandy soils under axial compression- parametric study”

Posted on 26 July 2023 by Don Warrington

As always I was gratified to be cited in the recent paper “3D FE analysis of bored pile- pile cap interaction in sandy soils under axial compression- parametric study,” by Faisal I. Shalabi, Mohammad U. Saleem, Hisham J. Qureshi, Md Arifuzzaman, Kaffayatullah Khan, and Muhammad M. Rahman. It is an interesting study of the topic at hand. Some comments are in order:

Although the citation is of Closed Form Solution of the Wave Equation for Piles, the work Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles is really closer to the methodology shown in the paper, both in terms of the 3D FEA used (well, I took a shortcut and used axisymmetric 2D analysis) and to the use of Mohr-Coulomb theory for the analysis, which I discuss in An Overview of Mohr-Coulomb Failure Theory and Elasto-Perfect Plasticity with Mohr-Coulomb Failure. Mohr-Coulomb is still viable for many applications, especially with sands.
One especially interesting aspect of this study was the inclusion of a pile cap. The problem is similar to the the one I discuss in my post When Semi-Infinite Spaces Aren’t, and When Foundations are Neither Rigid Nor Flexible, where the foundation is neither perfectly flexible relative to the soil nor perfectly rigid. Although in this study the foundation rigidity is not varied, the soil’s is, and as is the case in elastic theory as the soil becomes less rigid the relative rigidity of the foundation increases, the soil stresses relative to the foundation towards the edge of the foundation likewise increase. This Fall I plan to include that elastic theory in my discussion of mat foundations here: Foundation Design and Analysis: Shallow Foundations, Other Topics.
I noted a drop in the shaft friction just before the toe, followed by an increase down to the toe itself. The interaction between pile, soil and shaft friction for deep foundations is a complicated one. The toe creates failure surfaces in the soil that are certainly there–and it is reasonable to assume that they affect the shaft friction near the toe as well–but they are not exactly like those generated in shallow foundations, something which has complicated toe resistance calculations for a long time. The relative uniformity of the unit toe resistance makes sense based on failure theories going back to at least Vesić’s work in the early 1970’s. One thing that bored piles do not have to consider is the effects of advancement due to impact which, as Mark Randolph’s work has shown, almost show a “leading edge” effect.

It is my opinion that 3D FEA will ultimately be our best tool for estimating the load/settlement characteristics of deep foundations–bored or driven, static or dynamic–and this paper is a step forward in that regard.