Academic Issues – Page 8 – vulcanhammer.net

Constitutive Elasticity Equations: Three-Dimensional Formulation

Posted on 5 July 20226 July 2022 by Don Warrington

This is the beginning of what hopefully will be an enlightening series on elasticity and plasticity, primarily as it appears in finite element code. It is taken from a number of sources, including (but not limited to) Owen and Hinton (1980), Smith and Griffiths (1988) and Cook, Malkus and Plesha (1989.) Although finite element code has certainly advanced, the basics are still the same, especially with elasticity (plasticity is another matter.) More information on finite element analysis in geotechnics (with a link to Owen and Hinton) can be found here.

The basic elasticity relationship is familiar to engineers and can be stated as follows:

$\sigma = E \epsilon$ (1)

where

$\sigma =$ stress
$E =$ Young’s modulus, or modulus of elasticity
$\epsilon =$ strain

Element with normal and shear stresses (from Belyaev (1979))

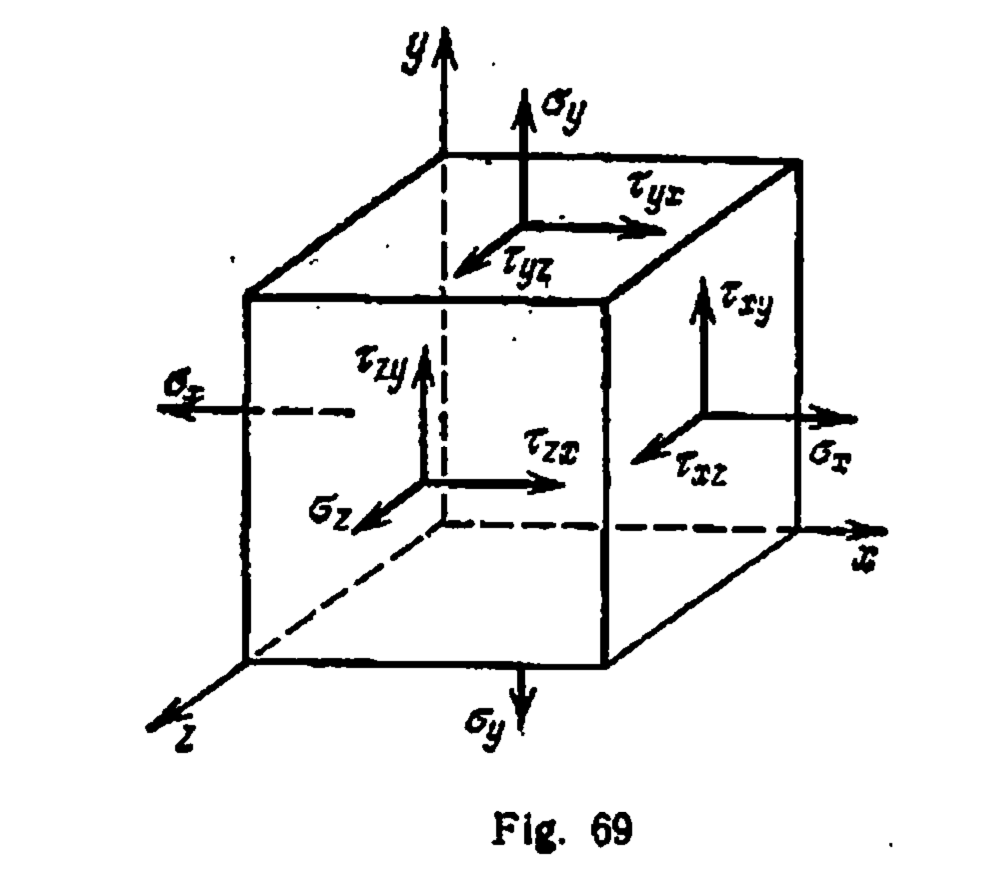
It can be used in one-dimensional analyses such as tension and compression testing; we’ll come back to that later. But real problems are always in three dimensions in one way or another. Let’s start by considering an infinitesimal element (these are discussed in Verruijt) that looks like the one in Figure 69. There are many ways of looking at this element. For one thing, it is in static equilibrium, which means that the stresses can be changed along with the coordinate system and the results still be in static equilibrium. Related to this is the fact that there is one coordinate system at which point the shear stresses vanish and the three normal stresses that are left are the principal stresses; this is discussed here.

These, however, are not our main interest here. Our main interest is how the element deforms under stress. For now we will restrict our discussion to elastic, path-independent stresses. We will rewrite Equation (1) is a slightly different form:

$D \epsilon = \sigma$ (2)

Now both $\sigma$ and $\epsilon$ are vectors; you can see the multiple stresses in Figure 69. We use the notation $D$ because the modulus of elasticity $E$ is a material property and thus is a part of the elasticity matrix $D$ .

In any case, when the actual vector and matrices are substituted into Equation (2), for three-dimensional problems such as shown in Figure 69 the equations look like this:

$\left[\begin{array}{cccccc} {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & 0 & 0 & 0\\ \noalign{\medskip}{\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & 0 & 0 & 0\\ \noalign{\medskip}{\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\nu}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(1-2\,\nu\right)}} & 0 & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(2-2\,\nu\right)}} & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(2-2\,\nu\right)}} & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & 0 & {\frac{{\it E}\,\left(1-\nu\right)}{\left(1+\nu\right)\left(2-2\,\nu\right)}} \end{array}\right]\left[\begin{array}{c} \epsilon_{{x}}\\ \noalign{\medskip}\epsilon_{{y}}\\ \noalign{\medskip}\epsilon_{{z}}\\ \noalign{\medskip}\gamma{}_{{\it xy}}\\ \noalign{\medskip}{\it \gamma}_{{\it yz}}\\ \noalign{\medskip}{\it \gamma}_{{\it zx}} \end{array}\right]=\left[\begin{array}{c} \sigma_{{x}}\\ \noalign{\medskip}\sigma_{{y}}\\ \noalign{\medskip}\sigma_{{z}}\\ \noalign{\medskip}\tau_{{\it xy}}\\ \noalign{\medskip}\tau_{{\it yz}}\\ \noalign{\medskip}\tau_{{\it zx}} \end{array}\right]$ (3)

It should be immediately apparent that there are many repetitious quantities. There are many ways of dealing with the problem. For this analysis we will substitute Lamé’s constants, which are

$\lambda = \frac{\nu E}{(1+\nu)(1-2\nu)}$ (4)

$G = \frac{E}{2(1+\nu)}$ (5)

where $\nu$ is Poisson’s Ratio and $G$ is the shear modulus of elasticity. The latter is very useful in soil mechanics (which can be seen, for example, here) and in fact Equation (4) can be restated as follows:

$\lambda = \frac{2\nu G}{1-2\nu}$ (6)

At this point we need to observe one important thing: no matter whether you use Equation (4) or (6), the Lamé constant $\lambda$ blows up (or becomes singular, as we say in polite circles) when $\nu = \frac{1}{2}$ . Materials where this is the case (such as very soft clays) are in reality fluids, the normal stresses become equal and the shear stresses only appear when the fluid moves. Avoiding this condition is one of the challenges of geotechnical finite element analysis.

It’s also worth noting that this is the same Lamé who came up with the theory behind shrink fits that is important with Vulcan hammers.

In any case, if we apply Equations (5) and (4) or (6), we obtain the following:

$\left[\begin{array}{cccccc} {\frac{\left(1-\nu\right)\lambda}{\nu}} & \lambda & \lambda & 0 & 0 & 0\\ \noalign{\medskip}\lambda & {\frac{\left(1-\nu\right)\lambda}{\nu}} & \lambda & 0 & 0 & 0\\ \noalign{\medskip}\lambda & \lambda & {\frac{\left(1-\nu\right)\lambda}{\nu}} & 0 & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & G & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & G & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & 0 & G \end{array}\right] \left[\begin{array}{c} \epsilon_{{x}}\\ \noalign{\medskip}\epsilon_{{y}}\\ \noalign{\medskip}\epsilon_{{z}}\\ \noalign{\medskip}\gamma{}_{{\it xy}}\\ \noalign{\medskip}{\it \gamma}_{{\it yz}}\\ \noalign{\medskip}{\it \gamma}_{{\it zx}} \end{array}\right]=\left[\begin{array}{c} \sigma_{{x}}\\ \noalign{\medskip}\sigma_{{y}}\\ \noalign{\medskip}\sigma_{{z}}\\ \noalign{\medskip}\tau_{{\it xy}}\\ \noalign{\medskip}\tau_{{\it yz}}\\ \noalign{\medskip}\tau_{{\it zx}} \end{array}\right]$ (7)

We see from this that we have simplified assembling the constitutive matrix considerably. From a coding standpoint, doing this eliminates not only the possibility of coding error but also computational cost by eliminating the sheer number of operations. This is especially useful if these matrices are reconstituted during the analysis (as one would expect if strain-softening is applied, for example.)

If we multiply the left hand side through, we have

$\left[\begin{array}{c} \sigma_{{x}}\\ \noalign{\medskip}\sigma_{{y}}\\ \noalign{\medskip}\sigma_{{z}}\\ \noalign{\medskip}\tau_{{\it xy}}\\ \noalign{\medskip}\tau_{{\it yz}}\\ \noalign{\medskip}\tau_{{\it zx}} \end{array}\right] = \left[\begin{array}{c} {\frac{\left(1-\nu\right)\lambda\,\epsilon_{{x}}}{\nu}}+\lambda\,\epsilon_{{y}}+\lambda\,\epsilon_{{z}}\\ \noalign{\medskip}\lambda\,\epsilon_{{x}}+{\frac{\left(1-\nu\right)\lambda\,\epsilon_{{y}}}{\nu}}+\lambda\,\epsilon_{{z}}\\ \noalign{\medskip}\lambda\,\epsilon_{{x}}+\lambda\,\epsilon_{{y}}+{\frac{\left(1-\nu\right)\lambda\,\epsilon_{{z}}}{\nu}}\\ \noalign{\medskip}G{\it \gamma}_{{\it xy}}\\ \noalign{\medskip}G{\it \gamma}_{{\it yz}}\\ \noalign{\medskip}G{\it \gamma}_{{\it zx}} \end{array}\right]$ (8)

Inversely, if we want to know the strains, we would compute these by the relationship

$\epsilon = D^{-1} \sigma$ (9)

Inverting,

$D_{e}^{-1}=\left[\begin{array}{cccccc} -{\frac{\nu}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & {\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & {\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & 0 & 0 & 0\\ \noalign{\medskip}{\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & -{\frac{\nu}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & {\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & 0 & 0 & 0\\ \noalign{\medskip}{\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & {\frac{{\nu}^{2}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & -{\frac{\nu}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}} & 0 & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & {G}^{-1} & 0 & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & {G}^{-1} & 0\\ \noalign{\medskip}0 & 0 & 0 & 0 & 0 & {G}^{-1} \end{array}\right]$ (10)

and the strains can be computed as follows

$\left[\begin{array}{c} \epsilon_{{x}}\\ \noalign{\medskip}\epsilon_{{y}}\\ \noalign{\medskip}\epsilon_{{z}}\\ \noalign{\medskip}\gamma{}_{{\it xy}}\\ \noalign{\medskip}{\it \gamma}_{{\it yz}}\\ \noalign{\medskip}{\it \gamma}_{{\it zx}} \end{array}\right] = \left[\begin{array}{c} -{\frac{\nu\,\sigma_{{x}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}+{\frac{{\nu}^{2}\sigma_{{y}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}+{\frac{{\nu}^{2}\sigma_{{z}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}\\ \noalign{\medskip}{\frac{{\nu}^{2}\sigma_{{x}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}-{\frac{\nu\,\sigma_{{y}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}+{\frac{{\nu}^{2}\sigma_{{z}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}\\ \noalign{\medskip}{\frac{{\nu}^{2}\sigma_{{x}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}+{\frac{{\nu}^{2}\sigma_{{y}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}-{\frac{\nu\,\sigma_{{z}}}{\lambda\,\left(-1+\nu+2\,{\nu}^{2}\right)}}\\ \noalign{\medskip}{\frac{\tau_{{\it xy}}}{G}}\\ \noalign{\medskip}{\frac{\tau_{{\it yz}}}{G}}\\ \noalign{\medskip}{\frac{\tau_{{\it zx}}}{G}} \end{array}\right]$ (11)

Relationships such as Equations (8) and (11) will be more useful when we consider two-dimensional problems.

References

Cook, R.D., Malkus, D.S. and Plesha, M.E. (1989). Concepts and Applications of Finite Element Analysis, John Wiley & Sons, Inc., New York, NY
Owen, D.R.J., and Hinton, E. (1980). Finite Elements in Plasticity: Theory and Practice. Pineridge Press, Swansea, Wales.
Smith, I.M., and Griffiths, D.V. (1988). Programming the Finite Element Method. Second Edition. John Wiley & Sons, Chichester, England.

Note: after this was first posted, some errors were discovered. These were corrected with the assistance of Jaeger, J.C. and Cook, N.G.W. (1979) Fundamentals of Rock Mechanics. London: Chapman and Hall. This book has an excellent treatment of basic theoretical solid mechanics in general and elasticity in particular. Although they do not put the equations in matrix form, they do use the Lamé constants in their formulation, albeit in a different way than is done here. We apologise for any inconvenience or confusion.

“Locating and quantifying necking in piles through numerical simulation of PIT” cites my paper “Comparison of Numerical Methods to Closed Form Solution for Wave Equation Analysis of Piling”

Posted on 20 June 2022 by Don Warrington

This recent paper, authored by Tarek Salem, Atef Eraky and Abdallah Almosallamy, was published in Frattura ed Integrità Strutturale. You can obtain the paper here but the gist of it can be found in the preprint, which can be found here.

My original paper was a derivative of my master’s thesis Closed Form Solution of the Wave Equation for Piles. The paper cited can be downloaded here.

The paper states that I used three methods of prediction for wave propagation in piles (WEAP, ANSYS and the closed form solution via MAPLE) to obtain the solution. Although all three of these and more cannot be applied to all solutions, the idea that we can use a variety of software to solve this problem was an important point of the original research, and I hope that this idea will continue to be pursued.

Note on the graphic at the top: it is one of the figures in my original paper, reconstructed in colour from the original CAD drawing. Many of the graphics in my thesis and my paper were done in CAD; we’ve come a long way in computer graphics.

Academic Issues, Geotechnical Engineering

A Quick Preliminary Way to Determine Slope Stability

Posted on 16 June 2022 by Don Warrington

Slope stability for circular failure surfaces is one of those topics where, for a complete solution, solving the problem has involved a computer solution before there were computers. The problem is that it is necessary to a) discretise the problem before solving it, in this case using slices, and b) try a large number of circle centre locations before finding the right one. The problem is illustrated below.

Prediction of slope stability by circular-cylindrical slip surfaces (from Tsytovich (1976))

One common method has been to use charts. A commonly used group is the Janbu series of charts, one of which is shown below.

Janbu Chart for cohesive soil (from NAVFAC DM 7.01)

A simpler solution is presented by Tsytovich (1976). The equation proposed there is this:

${\it FS}=\tan(\phi)A+{\frac {cB}{{\it \gamma}\,h}}$ (1)

where

$FS =$ factor of safety
$\phi =$ internal frictional angle of the soil
$c =$ cohesion of the soil
$\gamma =$ unit weight of the soil
$A,B =$ coefficients given below, functions of $e$ and $h$
$e$ = distance from slope toe to hard underground layer (see Figure 78(b))
$h$ = height of slope from toe to top (see Figure 78(b))
$m$ = second number of slope ratio rise:run (see Figure 78(b))

It is also possible to solve for a maximum height, thus:

$h={\frac {cB}{{\it \gamma}\,\left ({\it FS}-\tan(\phi)A\right )}}$ (2)

Coefficients of A and B for Approximate Prediction of Stability of Slopes (from Tsytovich (1976))

As an example, consider a slope with an angle of 35 degrees and a height of 20′. The soil has an internal friction angle of 15 degrees, a cohesion of 600 psf and a unit weight of 120 pcf. Estimate the factor of safety against slope failure using the method described. For this slope e = 0, so assume the slip surface passes through the lower edge (toe) of the slope.

The slope ratio 1:m is the reciprocal of the tangent of the slope given. Taking the tangent and inverting it gives a slope ratio of 1:1.43. It can be seen by inspection that A = 2.64 and through interpolation B = 6.38. Direct substitution yields a factor of safety of 2.3.

As a comparison we use the Slope program from our Soil Mechanics Course, the results are shown below using Fellenius’ Method.

The factor of safety is very close. If we used Bishop’s Method in the program, we could expect the factor of safety to increase. One thing absent from this problem is the presence of water, which always complicates slope stability analysis.

If we consider the example problem from the Janbu chart above, Equation (1) reduces to the equation for FS on the chart provided that $B = N_o$ . Doing the linear interpolation yields $B = 6.05$ , which is higher than the $N_o = 5.8$ on the chart, or $FS = 1.26$ .

Obviously the method is not suitable for final design but it is interesting for producing preliminary results for a problem which has traditionally been computationally difficult.

Academic Issues, Geotechnical Engineering

Foundation Design and Analysis: Shallow Foundations, Bearing Capacity

Posted on 14 June 202230 April 2023 by Don Warrington

Other resources:

Note: this is an update from an earlier lecture, which actually combines two lectures as well. Some new equipment was used; however, the “live screen” method didn’t quite work out, which meant that I ended up putting the slides in the video during video editing. Since I point to the slides from time to time, this may end up with some awkward moments. I apologise for any inconvenience.

Academic Issues, Soil Mechanics

Manual For The Systematic Study Of The Regime Of Underground Waters – Altovskij, Konopljantsev — Mir Books

Posted on 13 June 2022 by Don Warrington

In this post, we will see the book Manual For The Systematic Study Of The Regime Of Underground Waters edited by M. Altovskij; A. Konopljantsev. About the book The manual, is divided into four chapters. The first chapter-general theoretical problems-treats underground water and its behaviour as a natural historical process reflecting certain peculiarities attendant upon […]
Manual For The Systematic Study Of The Regime Of Underground Waters – Altovskij, Konopljantsev — Mir Books