Geotechnical Engineering – Page 15

What is a Resultant in Geotechnical Engineering?

Posted on 11 December 202129 June 2024 by Don Warrington

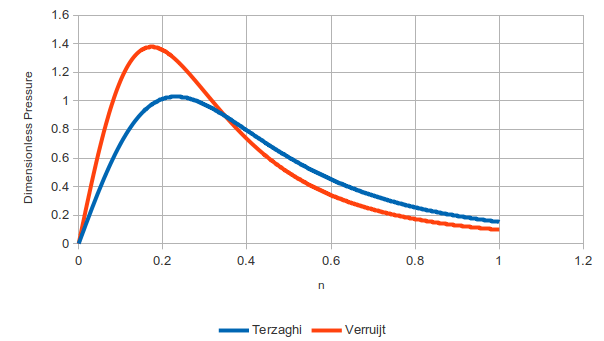
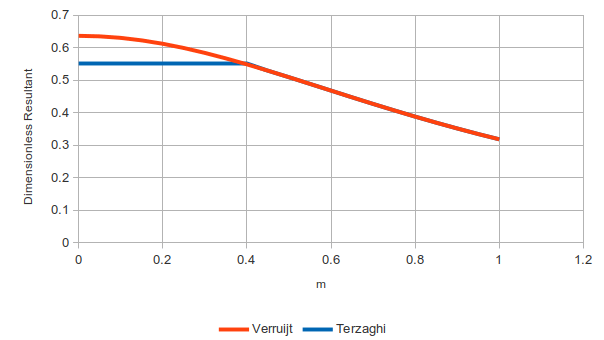
My students in Soil Mechanics and Foundations get introduced to some strange concepts. One of those is what I call the “old coot” method of statics, which I discuss here. Related to that is the concept of the “resultant.” Introduction of these concepts leads to puzzlement, which students generally hide in class, as many engineering students would make great professional poker players. But homework and tests do not lie…

Most all loads in geotechnical engineering are distributed loads, because they are the results of earth pressures, either horizontal (lateral) or vertical. Although most of these are either constant or ramped linear, the math with these gets complicated fast. In the past this was a major problem for geotechnical engineers armed with slide rules. The resultant is one way of simplifying the computations, and at the same time it offers better understanding of how earth pressures either load a structure or support it.

Let’s start with a definition: for most geotechnical problems, a resultant is a point load which is used to represent a distributed load. In general statics, the definition is broader, but this is what we’re going to discuss here. To accomplish this such a resultant must meet two criteria:

It must have the same total load as the distributed load.
It most pass through the centroid of the distributed load.

The example we’ll use here is from a previous post on braced cut analysis, a subject that has buffaloed many of my students over the years. The software layout of the wall, earth pressure loads, shears and moments is shown below.

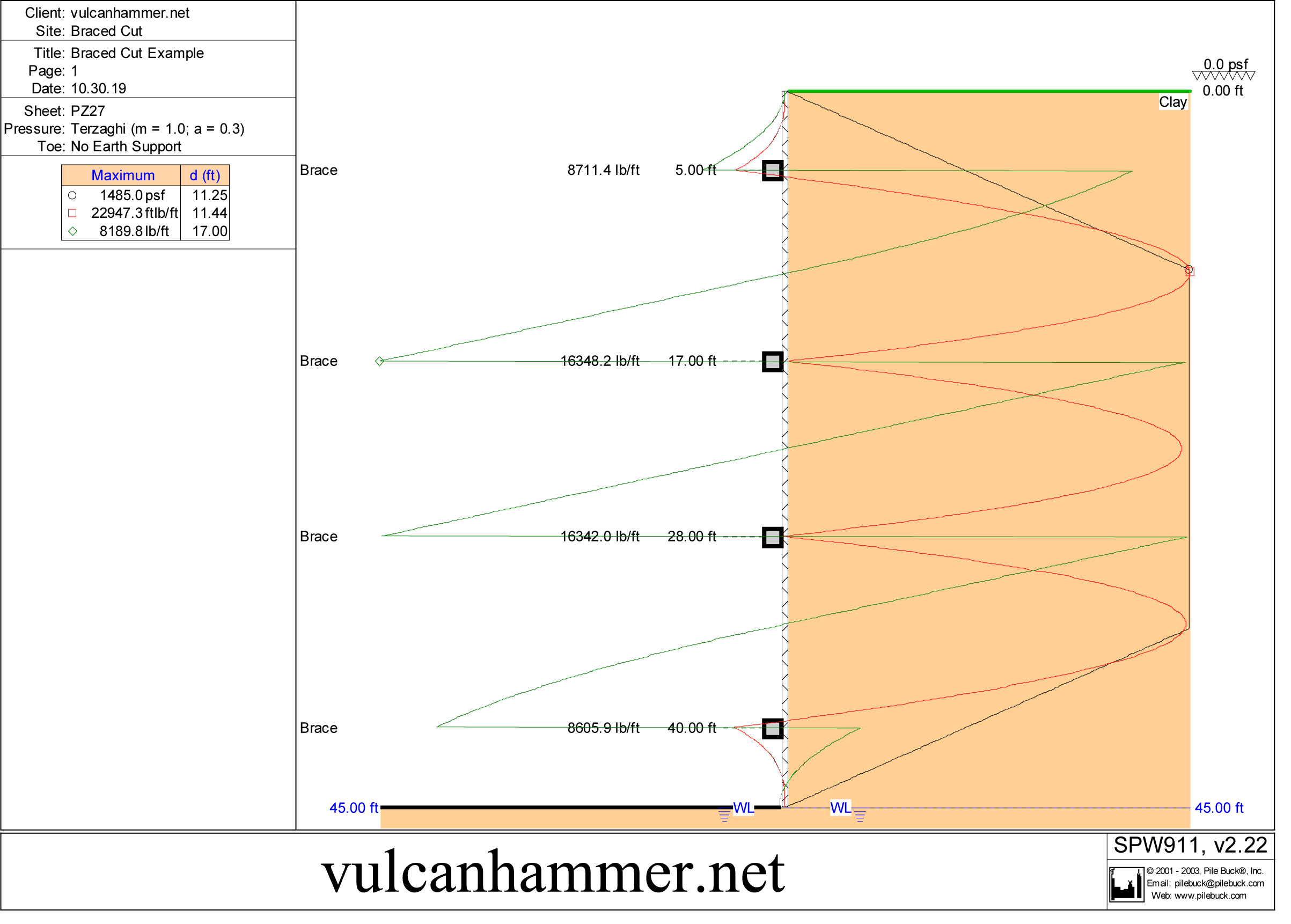
Using CFRAME to focus on the beam mechanics of the problem, first we will look at the model itself.

The basic layout of the model. The model is simply supported at all braces. Additionally–and this is one reason we wanted to use CFRAME–the central element 3 was additionally pinned at the ends to simulate Terzaghi and Peck’s original intent for the method.

The distributed loading is then shown below.

The pressure distribution on the model, replicating that Terzaghi and Peck distribution for stiff clays.

Let’s start with the easy section: the portion of the wall between 17′ and 28′ below the top of the wall (Element 3, between Nodes 3 and 4, shown in the basic layout.) As noted above, the beam has a distributed uniform of 1485 psf, or for our purposes 1485 lb/ft/ft of wall (vertical) and is simply supported on both ends. With this load the shear and moment looks like this, taken from the CFRAME program:

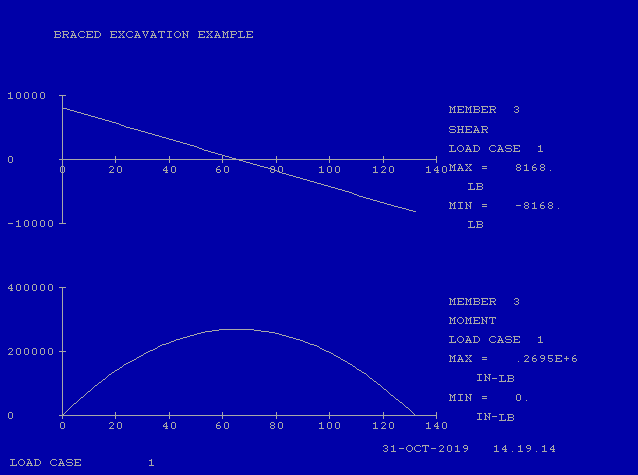
The way Terzaghi and Peck set this method forth, the beams at the top and bottom of the wall would be considered to be cantilever beams and the rest simply supported beams. This turns the whole problem into a statically determinate one, necessary to simplify the calculations. The diagram above shows a reaction of 8168 lbs. at each end, a maximum moment of 269,500 in-lb at the centre, and zero moment at the supports (due to the simply supported assumption.)

We could obtain this result by hand calculations. First, the reactions at the supports are given by the formula

$R = \frac{wl}{2} = \frac{1485 \times 11}{2} = 8168 \frac{lb}{ft}$ (1)

which is the same as above. The maximum moment is given by the equation

$M_{max} = \frac{wl^2}{8} = \frac{1485 \times 11^2}{8} = 22,461 \frac{ft-lb}{ft} = 269,528 \frac{in-lb}{ft}$ (2)

which is also the same as above.

Note: one of my students got very put out with me because I had the bad taste to say that these formulas were in the "steel book," the AISC Steel Construction Manual.  While I realise that it's hard to find anything in the steel book, they are there, and have been since the days I first used it at the Special Products Division.

Now let’s replace the distributed load by a resultant point load. Since the load is uniformly distributed, the centroid is at the centre of the beam. The resultant is

$F_{res} = wl = 1485 \times 11 = 16,335 \frac{lb}{ft}$ (3)

The reactions are computed by symmetry as follows:

$R = \frac{F_{res}}{2} = \frac{16335}{2} = 8168 \frac{lb}{ft}$ (4)

and the maximum moment (at the centre of the beam) is

$M_{max} = \frac{F_{res}l}{4} = \frac{16,335 \times 11}{4} = 44,921 \frac{ft-lb}{ft} = 539,055 \frac{in-lb}{ft}$ (5)

The reactions at the braces are the same. Thus, for the design of the braces, the methods give the same result. The maximum moment from the resultant, however, is twice the moment from a point load resultant. In practice one could deal with this problem by a) assuming the uncertainty in the earth loads justifies the conservatism of the resultant, b) scaling down the anticipated moment by noting the differences between the two (which are in turn the result of the statics of simply supported beams) or c) a combination of the two. In any case the need to use a resultant here isn’t great because of the uniform load.

Things get more complicated when we consider the second segment from the top, from 5′ to 17′. This 12′ long segment has the following pressure distribution:

At the top end of the beam, the pressure is 660 psf.
The pressure ramps up linearly to the maximum pressure of 1485 psf at a point 6.25′ from the end of the beam.
From this point until the bottom end of the beam 12′ from the top the pressure is uniform at 1485 psf.

Although it’s possible to get resultants from ramped load, it’s easier to divide a ramped load into a constant portion (minimum pressure) and a triangle load from zero to the difference between the minimum and maximum pressures. That being the case, the three regions are as follows, with their resultants:

The upper uniform region has a pressure of 660 psf and a length of 6.25′, thus its resultant is (660)(6.25) = 4125 lb/ft
The triangular region has a maximum pressure of 1485-660=825 psf, thus its resultant is (825)(6.25)/2 = 2578 lb/ft. The division by 2 is because it’s a triangle load.
The lower uniform region has a pressure of 1485 psf and a length of 12-6.25 = 5.75′, thus its resultant is (1485)(5.75) = 8539 lb/ft.

The location of these resultants is as follows:

The upper uniform region is half the length of the region, thus it is 6.25/2 = 3.125′ from the top end.
The upper triangular region is two-thirds the length of the region, thus it is 2*6.25/3 = 4.17′ from the top end
The lower uniform is the length of the upper region plus half the length of the lower region, thus it is 6.25 + 5.75/2 = 9.125′.

The reactions for a point load at any point in the beam are given by the equation

$R_1 = F_{res} (1-k)$ (6)

$R_2 = F_{res} k$ (7)

The variable k is the ratio of the distance from the top end of the resultant to the total beam length. We can add the contribution from each resultant to obtain total reactions.

Resultant	F_res, lb/ft	Location from top, ft	k	R₁	R₂
1	4125	3.125	0.26	3053	1073
2	2578	4.17	0.35	1676	902
3	8539	9.125	0.76	2046	6493
Total	15,242			6775	8468

It can be shown that the sum of the reactions is the same as the sum of the resultants within rounding error, as should be the case.

The maximum moment is a little more complicated. For any point load on a simply supported beam, the moment begins at zero at the support, linearly rises to a maximum of $F_{res} k (1-k)$ , and then linearly declines to zero at the opposite support. This means that each moment distribution needs to be determined at many points and then the result summed at each point to insure that the maximum moment is identified. The spreadsheet implementation of this is here and you can see the moment distribution for each resultant and their sums below. The maximum moment is 24,322 ft-lbs/ft = 291,869 in-lbs/ft.

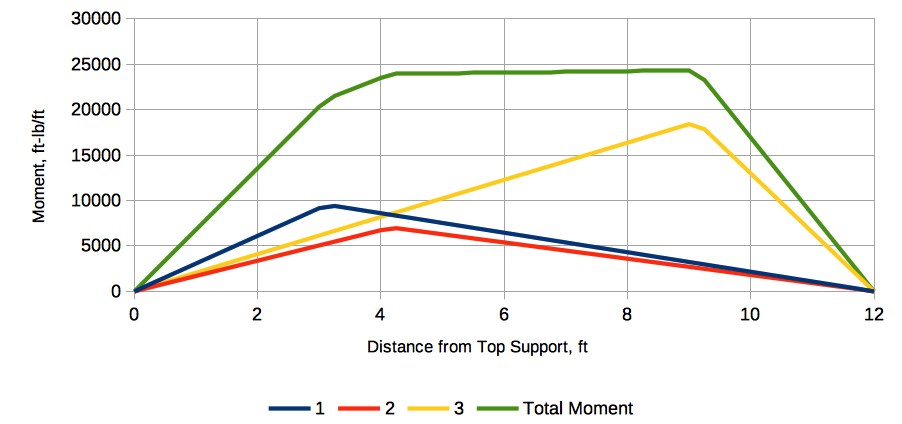
Now let’s compare this with the CFRAME results, which took into consideration distributed loads. Hand calculations for distributed loads are fairly involved.

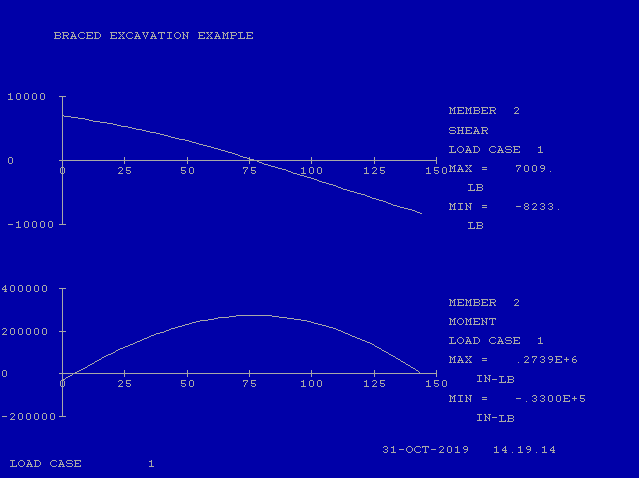
We’ll start with the moment. The maximum moment from CFRAME (273,900 in-lb/ft) is a little smaller that that which is predicted by the resultants. This is expected; the more resultants the load is divided into, the closer to the distributed load result the moment will become.

With the reactions, the sum of the reactions shown in CFRAME is identical to those from the resultant method; however, the reactions themselves are different. That’s because it is not possible to accurately reproduce a simply supported beam for Segment 2 and have a cantilever beam for Segment 1. In CFRAME we are forced to use a continuous beam from the top to the second brace (17′) and simply support them at both points. Note carefully that the moment at the left (top) end of the beam is nonzero, which is not the case with a simply supported beam. This illustrates that, from a structural standpoint, the method of Terzaghi and Peck for braced cuts is artificial, although it is possible to combine Segments 1 and 2 and do hand calculations for these with resultants.

It’s worth noting that the brace loads using SPW911 at 17′ and 28′ are 16,340 lb/ft of wall. If we use the resultant method, the brace loads (the structure is symmetric) should be 8468 + 8168 = 16,636 lb/ft and using CFRAME 8233 + 8168 = 16,401, neither of which are identical to SPW 911. This is a good illustration of the care you need to take when evaluating computer generated results.

Nevertheless, I think the use of resultants is adequately illustrated by this example. Perhaps in the future more examples of resultants can be given.

Geotechnical Engineering

Rankine and Coulomb Earth Pressure Coefficients

Posted on 28 September 202112 April 2025 by Don Warrington

For retaining walls, computing these is important; but the textbooks and reference books are frequently confusing and sometimes wrong. These formulae, derived using Maple, should clear up a few things, although they’re a) not always in the format you’re used to and b) subject to the Terms and Conditions of this site.

Let’s start with a diagram and the basic Coulomb formulae, from NAVFAC DM 7.02, shown above. It’s important for to have a nomenclature chart for any lateral earth pressure coefficient formulae.

Coulomb Active Coefficients

All angles nonzero:

$K_{{a}}=\left (\cos(-\phi+\theta)\right )^{2}\left (\cos(\theta)\right )^{-2}\left (\cos(\theta+\delta)\right )^{-1}\left (1+\sqrt {-{\frac {\sin(\phi+\delta)\sin(-\phi+\beta)}{\cos(\theta+\delta)\cos(\theta-\beta)}}}\right )^{-2}$ (1a)

Vertical Wall:

$K_{{a}}=\left (\cos(\phi)\right )^{2}\left (\cos(\delta)\right )^{-1}\left (1+\sqrt {{\frac {\sin(\phi+\delta)\sin(\phi-\beta)}{\cos(\delta)\cos(\beta)}}}\right )^{-2}$ (1b)

Level Backfill:

$K_{{a}}=\left (\cos(-\phi+\theta)\right )^{2}\left (\cos(\theta)\right )^{-2}\left (\cos(\theta+\delta)\right )^{-1}\left (1+\sqrt {{\frac {\sin(\phi+\delta)\sin(\phi)}{\cos(\theta+\delta)\cos(\theta)}}}\right )^{-2}$ (1c)

Vertical Wall and Level Backfill:

$K_{{a}}={\frac {\left (\cos(\phi)\right )^{2}}{\left (\sqrt {\cos(\delta)}+\sqrt {\sin(\phi+\delta)}\sqrt {\sin(\phi)}\right )^{2}}}$ (1d)

Coulomb Passive Coefficients

All angles nonzero:

$K_{{p}}=\left (\cos(\phi+\theta)\right )^{2}\left (\cos(\theta)\right)^{-2}\left (\cos(\theta-\delta)\right )^{-1}\left (1-\sqrt {{\frac {\sin(\phi+\delta)\sin(\phi+\beta)}{\cos(\theta-\delta)\cos(\theta-\beta)}}}\right )^{-2}$ (1e)

Vertical Wall:

$K_{{p}}={\frac {\left (\cos(\phi)\right )^{2}\cos(\beta)}{\cos(\beta)\cos(\delta)-2\,\sqrt {\cos(\beta)}\sqrt {\cos(\delta)}\sqrt {\sin(\phi+\beta)}\sqrt {\sin(\phi+\delta)}+\sin(\phi+\beta)\sin(\phi+\delta)}}$ (1f)

Level Backfill:

$K_{{p}}={\frac {\left (\cos(\phi+\theta)\right )^{2}}{\cos(\theta)\left (\cos(\theta)\cos(\theta-\delta)-2\,\sqrt {\cos(\theta)}\sqrt {\cos(\theta-\delta)}\sqrt {\sin(\phi+\delta)}\sqrt {\sin(\phi)}+\sin(\phi+\delta)\sin(\phi)\right )}}$ (1g)

Vertical Wall and Level Backfill:

$K_{{p}}=-{\frac {\left (\cos(\phi)\right )^{2}}{-\cos(\delta)+2\,\sqrt {\cos(\delta)}\sqrt {\sin(\phi+\delta)}\sqrt {\sin(\phi)}-\sin(\phi+\delta)\sin(\phi)}}$ (1h)

Rankine Active Coefficients

These were derived assuming that Rankine coefficients are the same as their Coulomb counterparts except for $\delta = 0$ ). This is strictly speaking not the case and will be discussed in detail below.

Sloping Wall and Backfill:

$K_{{a}}=\left (\cos(\phi-\theta)\right )^{2}\left (\cos(\theta)\right)^{-3}\left (1+\sqrt {{\frac {\sin(\phi)\sin(\phi-\beta)}{\cos(\theta)\cos(\theta-\beta)}}}\right )^{-2}$ (2a)

Vertical Wall:

$K_{{a}}=\left (\cos(\phi)\right )^{2}\left (1+\sqrt {{\frac {\sin(\phi)\sin(\phi-\beta)}{\cos(\beta)}}}\right )^{-2}$ (2b)

Level Backfill:

$K_{{a}}=\left (\cos(\phi-\theta)\right )^{2}\left (\cos(\theta)\right)^{-3}\left (1+\sqrt {{\frac {\left (\sin(\phi)\right )^{2}}{\left (\cos(\theta)\right )^{2}}}}\right )^{-2}$ (2c)

Vertical Wall and Level Backfill:

$K_{{a}}={\frac {\left (\cos(\phi)\right )^{2}}{\left (1+\sin(\phi)\right )^{2}}}$ (2d)

Rankine Passive Coefficients

$K_{{p}}=\left (\cos(\phi+\theta)\right )^{2}\left (\cos(\theta)\right)^{-3}\left (1-\sqrt {{\frac {\sin(\phi)\sin(\phi+\beta)}{\cos(\theta)\cos(\theta-\beta)}}}\right )^{-2}$ (2e)

Vertical Wall:

$K_{{p}}=-{\frac {\left (\cos(\phi)\right )^{2}\cos(\beta)}{-\cos(\beta)+2\,\sqrt {\cos(\beta)}\sqrt {\sin(\phi+\beta)}\sqrt {\sin(\phi)}-\sin(\phi+\beta)\sin(\phi)}}$ (2f)

Level Backfill:

$K_{{p}}=-{\frac {\left (\cos(\phi+\theta)\right )^{2}}{\cos(\theta)\left (-\left (\cos(\theta)\right )^{2}+2\,\cos(\theta)\sin(\phi)-1+\left (\cos(\phi)\right )^{2}\right )}}$ (2g)

Vertical Wall and Level Backfill:

$K_{{p}}={\frac {\left (\cos(\phi)\right )^{2}}{\left (-1+\sin(\phi)\right )^{2}}}$ (2h)

The Origin of Rankine Earth Pressure Coefficients

It is a matter of record that Rankine earth pressure coefficients were derived from a combination of Mohr-Coulomb failure theory and the effect of wall movement on the horizontal earth pressure. The physical manifestation of the theory is illustrated at the right, based on tests which have been run over the years.

OTOH, Coulomb earth pressures were derived from the static equilibrium of a soil wedge (with a failure surface, see diagram at left.)

The thing that has confused the issue is that, for the case of level backfill, vertical wall and no wall friction, the results of Equations (2d) and (2h) are identical with the Rankine theory results as originally derived. This equivalence is doubtless more than fortuitous but it does not necessarily extend upwards to the other cases.

This has been recognised for a long time. For the case of the vertical wall and sloping backfill, the application of “conjugate stresses” (Hough, 1970) as opposed to principal stresses results in the following “Rankine” earth pressure coefficient:

$K_{{a}}={\frac {\cos(\beta)\left (\cos(\beta)-\sqrt {\left (\cos(\beta)\right )^{2}-\left (\cos(\phi)\right )^{2}}\right )}{\cos(\beta)+\sqrt {\left (\cos(\beta)\right )^{2}-\left (\cos(\phi)\right )^{2}}}}$ (3)

and its passive counterpart

$K_{{a}}={\frac {\cos(\beta)\left (\cos(\beta)+\sqrt {\left (\cos(\beta)\right )^{2}-\left (\cos(\phi)\right )^{2}}\right )}{\cos(\beta)-\sqrt {\left (\cos(\beta)\right )^{2}-\left (\cos(\phi)\right )^{2}}}}$ (4)

Ebeling and Morrison (1992) note the following about Equation (3):

The Rankine active earth pressure coefficient for a dry frictional backfill inclined at an angle $\beta$ from horizontal is determined by computing the resultant forces acting on vertical planes within an infinite slope verging on instability, as described by Terzaghi (1943) and Taylor (1948).

Equations (2b) and (3) reduce to Equation (2d) and Equations (2f) and (4) reduce to Equation (2h) when $\beta = 0$ .

A quick comparison was made by dividing the right hand side of Equation (3, numerator) by the right hand side of Equation (2b, denominator.) A survey of the results are shown below. The angles are shown on the x- and y-axes in radians; the friction angle $\phi$ varies from 30 to 45 degrees and the backfill angle $\beta$ varies from 5 to 15 degrees. The result shows that the Terzaghi and Taylor (an interesting combination to say the least) coefficients are slightly lower than the Coulomb derived coefficients.

It’s a completely different story with the passive coefficients; dividing the right hand side of Equation (4) by the right hand side of Equation (2f) with the same angle ranges as above gives us the following result:

As an interesting side note, if we take a test case of φ = 30 deg. and β = 10 deg., the passive coefficient using Equation (4) is actually less than the one for level backfill!

This is a topic that deserves further investigation; however, extending Rankine theory using Coulomb wedge theory without wall friction has merit for those applications (such as vinyl or fibreglass sheet piling) where inclusion of wall friction is inappropriate to the application.

References

Ebeling, R.M., and Morrison, E.E. Jr. (1992) The Seismic Design of Waterfront Retaining Structures. Technical Report ITL-92-11. Vicksburg, MS: U.S. Army Waterways Experiment Station.

Hough, B.K. (1970) Basic Soils Engineering. Second Edition. New York: The Ronald Press Company.

Geotechnical Engineering, Pile Driving Equipment

Vulcan and Sheet Piling — vulcanhammer.info

Posted on 21 September 2021 by Don Warrington

The development of sheet piling and the Warrington-Vulcan hammers was about the same time (along with concrete piles, other types of steel piles, and the Engineering News Formula.) The years leading up to World War I were ones of rapid development in the marine construction and deep foundation industries, and Vulcan was in the middle […]
Vulcan and Sheet Piling — vulcanhammer.info

Geotechnical Engineering

The Difference Between Flamant’s and Terzaghi’s Solution for Line Loads Behind Retaining Walls

Posted on 9 September 2021 by Don Warrington

Generally speaking, in Soil Mechanics courses elastic solutions on semi-infinite half spaces are presented to allow the geotechincal engineer to estimate the stresses induced in a soil by a load at the surface. Also presented in Soil Mechanics courses are charts and equations to estimate the lateral pressures on retaining walls induced by vertical loads on the surface behind the retaining walls. How either of these came into being is generally not explained; additionally, the fact that they are related is not explained either. The purpose of this article is to explain that relationship and, in the case of the retaining walls, how the original equations have been modified to suit experimental data. For simplicity’s sake, the discussed will be restricted to line loads.

The Original Equations: Flamant

As pointed out by Verruijt, the original equation for the stresses (vertical, horizontal and shear) were first set forth by Flamant in 1892. The equations are shown below.

Flamant Solution for a Line Load on a Semi-Infinite Elastic Medium, from Verruijt

The derivation of this equation can be found here or in Verruijt. Note carefully that the vertical load induces stresses in the horizontal direction (and in shear) as well as the vertical direction.

Verruijt then shows the following:

Mirror Flamant Loads on either side of an arbitrary dividing line and the computation of stress against a rigid wall.

Basically, by static equilibrium, if you replace the left half of the two mirrored loads (on the left) with a rigid wall, the horizontal stresses would be the same on the centre axis/wall as induced by two line loads. The resulting stresses and the resultant for the stress distribution are given below.

Flamant’s Equation for Horizontal Stresses Against a Rigid Wall, Including the resultants

The Modified Equations: Terzaghi

Generally, however, these equations are not presented in books such as DM 7, Sheet Pile Design by Pile Buck or others in this exact form. The following chart (frequently copied) comes from the Soils and Foundations Manual:

The line load is in the upper right hand corner. For values of m (the ratio of the distance from the line load to the wall over the height of the wall) greater than or equal to 0.4, the two results are the same. For those less than that, they are different. (In Verruijt’s notation, m = a/z.) The difference is because most books use the formulation of Terzaghi (1954). He explains the difference as follows:

However, the application of the line load tends to produce a lateral deflection of the vertical section, and the flexural rigidity of the bulkhead interferes with that deflection…However, for values smaller than (m=)0.4, the discrepancy between observed and computed values increases with decreasing values values of m…
From Terzaghi, K. (1954) “Anchored Bulkheads.” Transactions of the American Society of Civil Engineers, Vol. 119, Issue 1.

The whole issue of the flexibility of the retaining wall has been the chief complicating factor in this discussion, going back to Spangler’s tests in the 1930’s.

Comparing the Two Solutions

As an illustration, consider the pressure distribution situation when m=0.3:

Comparison of Flamant/Verruijt and Terzaghi Solutions for Line Load Pressures, m = 0.3

The pressures have been made dimensionless for generalisation. The Flamant solution comes to a higher peak nearer to the surface but falls off more rapidly down the wall. Terzaghi’s solution is more evenly distributed.

Now consider the situation at m=0.5:

Comparison of Flamant/Verruijt and Terzaghi Solutions for Line Load Pressures, m = 0.5

The two are identical in this range.

We can also consider the resultants as well:

Comparison of Flamant/Verruijt and Terzaghi Solutions for Line Load Resultants

The y-axis is made dimensionless by dividing the resultant by the vertical line load. For values of m less than or equal to 0.4, the results are different; for greater, they are the same.

In general, we can say that Flamant’s original formulation is more conservative. In the event that a deeper understanding of the interaction of surface loads with a retaining wall is desired, a finite element analysis needs to be done.

Geotechnical Engineering

Deep Foundations Magazine July/August Issue

Posted on 26 August 2021 by Don Warrington

Did you miss the July/August 2021 issue of Deep Foundations Magazine by the Deep Foundations Institute (DFI)? Not to worry, we’ve got you covered. …
Deep Foundations Magazine July/August Issue