Closing the Loop (or at least trying to) on Hough’s Settlement Method

My post Getting to the Legacy of B.K. Hough and his Settlement Method got a good amount of interest. Unfortunately it left several “loose ends,” some of which is because we don’t have full information on some of Hough’s methodology, and others because we don’t have full information on the FHWA’s thinking in their resurrection of the method. The objective of this post is to clear up some of these loose ends, especially the latter.

What we needed was some additional information on the background for both Hough’s work and the FHWA’s interpretation of that work. That information came from an unexpected source: the FHWA’s Design and Construction of Driven Pile Foundations, 2016 Edition. This has been available on vulcanhammer.info just about since it was first published. Now some of you are asking, “Why is this guy waiting until now to come out with stuff he’s had for years? Doesn’t he read the material he offers for download?” In my defence, I didn’t expect the solution to come from the driven pile manual, since it’s primarily a shallow foundation issue. It’s there because it’s proposed for use with groups of driven piles in cohesionless soils.

With all that said let’s look at some of the issues this “new” source tackles.

The SPT Correction Issue

The basic equation for Hough’s method is similar to that used for one-dimensional consolidation settlement and is

$S=\frac{H_{o}}{C'} \log_{10} \frac{\sigma'_f}{\sigma'_o}$ (1)

where

$S =$ settlement of cohesionless soil layer
$H_o =$ layer thickness
$C' =$ compression coefficient
$\sigma'_o =$ effective stress at the centre of the layer
$\sigma'_f =$ effective stress at the centre of the layer plus the induced stress from the surface at the centre of the layer

The tricky part has always been $C'$ . My criticisms of the FHWA’s implementation of the method in the post Getting to the Legacy of B.K. Hough and his Settlement Method were as follows:

Hough’s Method may or may not have used a 60% (N₆₀) efficient hammer to develop the method. It’s entirely possible but Hough (1959) doesn’t say what type of hammer he used to develop the method.
The FHWA implementation of Hough’s method included an SPT correction for overburden, which was absent in Hough (1959.)
An absence of any mention of Hough (1970,) where he modified the $C'$ values.
The lack of an attempt to convert the chart to equations. My original post demonstrates how this can be done, using the method of Hough (1970.)

Design and Construction of Driven Pile Foundations, 2016 Edition addresses all of this as follows:

Cheney and Chassie (2002) report that FHWA experience with this method indicates the method is usually conservative and can overestimate settlements by a factor of 2. This conservatism is attributed to the use of the original bearing capacity index chart from Hough (1959) which was based upon SPT donut hammer data. Based upon average energy variations between SPT donut, safety, and automatic hammers reported in technical literature, Figure 7-43 now includes a correlation between SPT N values from safety and automatic hammers and bearing capacity index. The safety hammer values are considered N60 values. This modification should improve the accuracy of settlement estimates with this method.

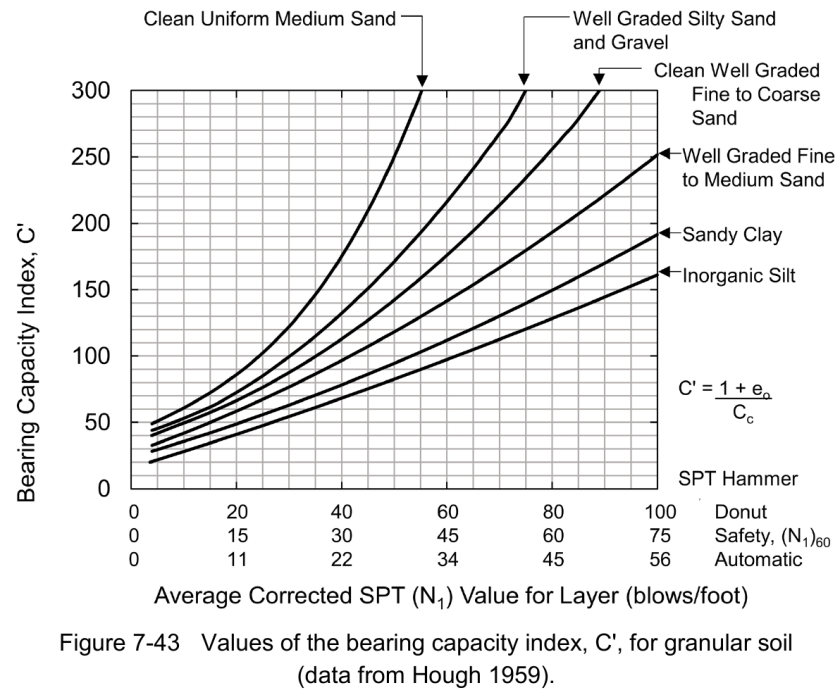
The following should be noted about these changes:

The assumption that Hough used a “donut” hammer is a reasonable one based on the technology of the time, but it’s still an assumption. Hough doesn’t tell us the kind of SPT hammer he used, or even how he came up with the C’ values shown above.
The chart above (Figure 7-43) shows the correlation for three types of hammers: donut, safety, and automatic hammers (which now “rule the roost” in testing.) However, it still insist that the safety hammer values should be corrected for overburden, something else absent from Hough’s study.
There is still no awareness of Hough (1970.)

So we can say that we have, perhaps, made some progress toward a solution, but at this point we are not quite where we would like to be.

My Thinking on the Way Forward

We usually think in terms of progress in this field in terms of peer-reviewed articles. But we’ve had the peer-reviewed articles, the experts weigh in on what they mean, and another set of experts try to make things better. My own solution to this problem would run like this:

Let’s accept the FHWA’s idea that Hough used a donut hammer for his original work. Donut hammers have a “standard” efficiency of 45%. To get the SPT blow counts to an N₆₀ value (60% efficiency) we need to divide the donut SPT values by 60/45 = 4/3. (That’s what’s going on in the graph above.)
Let’s use Hough’s method as he presented it in Hough (1970) and assume that those values too came from donut hammers.
Let’s lose the overburden correction; it wasn’t in the original and I don’t see how one can justify putting it into this method.

If we implement all of this, the chart now looks like this:

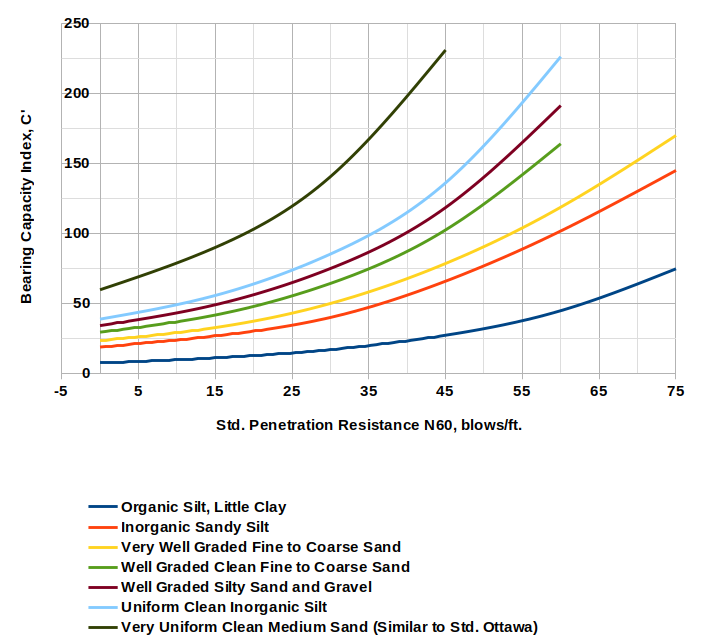
If formulae are preferred (and that’s normally the case these days) they will again be in the form

$C' = A \exp^{BN}$ (2)

and the coefficients will be as follows:

Soil Type	A	B
Organic Silt, Little Clay	7.22	0.0305
Inorganic Sandy Silt	18.27	0.0279
Very Well Graded Fine to Coarse Sand	22.86	0.0270
Well Graded Clean Fine to Coarse Sand	28.22	0.0289
Well Graded Silty Sand and Gravel	32.85	0.0289
Uniform Clean Inorganic Silt	37.02	0.0294
Very Uniform Clean Medium Sand (Similar to Std. Ottawa)	58.66	0.0299

The “B” coefficients run in a fairly narrow range and have an average of 0.0289. It’s possible using this or a more sophisticated method to apply the same value of B to all of the soils.

Any comments from those of you who have used Hough’s Method, or have research on the topic, would be greatly appreciated.

References

Hough, B.K. (1959). “Compressibilty as the Basis for Soil Bearing Value,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol. 85, Part 2.
Hough, B.K. (1970). Basic Soils Engineering. Second Edition. New York: Ronald Press Company.