NAVFAC DM 7.2: Analysis of Walls and Retaining Structures, Part I: Will the Real Rankine Theory Please Stand Up?

Now we get into a topic which has certainly been of interest to me, the co-author/editor of Sheet Pile Design by Pile Buck. I’m going to begin by tackling the subject of lateral earth pressure theories. NAVFAC DM 7.2‘s treatment of this subject is illuminating but raises many questions about how these relate to each other and to the design of retaining walls.

Acknowledging the Source of Jaky’s Equation

I’ll start with another topic, namely that of Jaky’s Equation, which is the “standard” for at-rest earth pressure theories. The first thing that comes up is the definition of the coefficient of earth pressure, given as

$K_o = \frac{\sigma'_h}{\sigma'_z}$ (4-1)

The hard truth here is that this is the definition of any lateral earth pressure coefficient; the difference is which theory is applied. It’s not just for at-rest earth pressures.

Turning to Jaky’s Equation, the equation for at-rest lateral earth pressure coefficients is given as

$K_o = (1-\sin\phi')OCR^{\sin\phi'}$ (4-2)

Obviously for normally consolidated soils (OCR = 1) this reduces to

$K_o = 1-\sin\phi'$

but this is Jaky’s Equation, which is the basis for Equation (4-2). I think that credit needs to be given to its originator as has been the case with textbooks and reference books for many years.

Will the Real Rankine Theory Please Stand Up?

Now we get to the interesting part: the nature of Rankine Theory. The fact that, for vertical walls with level backfill and no wall-soil friction, the lateral earth pressure equations for both Rankine and Coulomb theory are the same. This has led to a good deal of confusion on the subject, such as “Rankine theory is just Coulomb theory with no wall friction,” but this is not the case. Rankine Theory is based on the application of Mohr’s Circle, while Coulomb Theory has its origins in static equilibrium of soil wedges. NAVFAC DM 7.2 does a good job making this distinction but in the process a few observations are in order.

First, while NAVFAC DM 7.2 goes into detail on the level backfill/vertical wall case, it does not include the “extensions” developed for sloping backfill. It states that “…there are published techniques that can accommodate inclined backfills.” I discuss one of these in my post Rankine and Coulomb Earth Pressure Coefficients. Excluding these restricts the use of Rankine theory in the same way we see in, say, Tsytovich, except that provision for cohesion is included.

Pursuant to that inclusion, NAVFAC DM 7.2 redraws this diagram from DM 7.02 in this way:

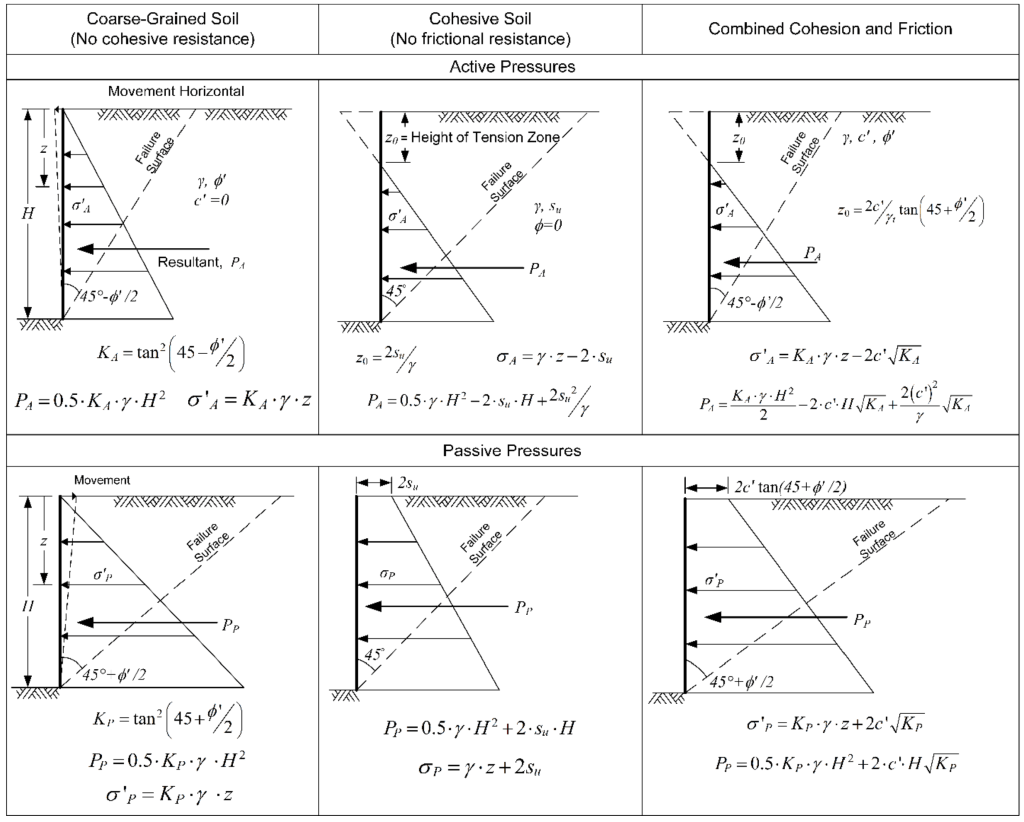
If they’re serious about making a clear distinction between Rankine and Coulomb theories, they need to eliminate the failure surfaces in the diagrams. I’m as aware as anyone of the role failure surfaces play in things such as anchor design, but it doesn’t change the basic nature of the theories. (I’m aware that there are rupture surfaces in Rankine theory, but they are different than wedge failure. Inclusion of a diagram such as is shown below (from this source) would have clarified the distinction.)

Finally, I don’t understand why they included the material on wall/soil interface friction angles in the section on Rankine theory, since Rankine theory doesn’t take into account wall/soil friction (it doesn’t consider soil/soil friction along a failure surface either.)

And as for Coulomb…

The presentation on Coulomb theory is similar to that in the old book with redrawn graphics and some tighter limits on acceptable limits of parameters such as wall friction and backfill angle. As was the case with the old book, NAVFAC DM 7.2 includes charts for vertical walls with sloping backfill and no wall friction for both the earth pressure coefficients and failure plane angle. And, like the old book, it doesn’t really explain why these charts are important. Should we ignore wall friction in many cases (the old book implied that we could for active pressures)? And how do the results of Coulomb theory under these conditions compare with the “Rankine extensions” with which the new book dispenses but are found in practice? (The answer to the last question can be found in the post Rankine and Coulomb Earth Pressure Coefficients.) I think that, with topics like this where there is significant variance in the way the theory is applied, DM 7 in general tends to “punt” on issues like these.

Coulomb earth pressure inevitably lead to the issue of trial wedge methods for complex geometries and stratigraphies. Personally I think that, with the advent of FEA, trial wedge methods are obsolete. NAVFAC DM 7.2 notes that “…finite element and finite difference soil structure interaction software can be used to solve these types of problems, but considerable skill is required to obtain meaningful results.” The same observation could be made about trial wedge methods. As someone who spent two decades in geotechinical education (and more if you include my work on this site) I don’t see the generation of engineers coming up developing the skill set for trial wedge methods.

Log-Spiral Methods

Log-spiral theory (especially in the passive case) has two significant advantages over Coulomb theory: it more accurately models the failure surface (FEA eliminates the need to do that, it figures it out for itself) and that in turn results in a smaller soil wedge and lower (less unconservative) earth pressure coefficients. Using these require a chart solution, and NAVFAC DM 7.2 makes a significant advance in that it abolishes the correction table for different values of $\frac{\delta}{\phi}$ and simply presents the chart for $\frac{\delta}{\phi} = \frac{2}{3}$ as a typical value. The new book expresses doubts about the accuracy of these correction factors, but there’s one thing for sure: it’s much less confusing and subject to error in use, and will make classroom teaching of this method much easier. My only concern about these is applying them to walls where soil/wall friction is minimal, as is the case with fibreglass and vinyl sheet piling.

The FHWA’s Solution

In its discussion of the log-spiral method, NAVFAC DM 7.2 states that (…passive pressure should be computed using the log spiral method and not the Coulomb method.” This is obviously due to the advantages of log-spiral methods discussed above. It’s worth noting (and the book should have done so) that the FHWA’s usual solution to this problem is to use Coulomb active/log-spiral passive combinations in practice, as they explain in the Soils and Foundations Reference Manual. This would have buttressed support for their case and given the engineer more definitive guidance in what can be a confusing topic.

Lateral earth pressure is the oldest analytic topic in geotechnical engineering; Coulomb published his paper in the same year the American colonies declared their independence from Great Britain. It is an indication of the nature of the field that we still do not have a firm consensus on how these are to be precisely computed and applied.