Comments on “Using the Impulse–Response Pile Data for Soil Characterization”

It’s citation time again; this paper, authored by Heeyong Huh, Heedong Goh, Jun Won Kang, Stijn François and Loukas F. Kallivokas, cites both Closed Form Solution of the Wave Equation for Piles and Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles. It is available here. The abstract is as follows:

The impulse–response (IR) test is the most commonly used field procedure for assessing the structural integrity of piles embedded in soil. The IR test uses the response of the pile to waves induced by an impulse load applied at the pile head in order to assess the condition of the pile. However, due to the contact between the pile and the soil, the recorded response at the pile head carries information not only about the pile, but about the soil as well, thus creating the as-yet-unexplored opportunity to characterize the properties of the surrounding soil. In effect, such dual use of the IR test data renders piles into probes for characterizing the near-surface soil deposits and/or soil erosion along the pile–soil interface. In this article, we discuss a systematic full-waveform-based inversion methodology that allows imaging of the soil surrounding a pile using conventional IR test data. We adopt a heterogeneous Winkler model to account for the effect of the soil on the pile’s response, and the pile’s end is assumed to be elastically supported, thus also accounting for the underlying soil. We appeal to a partial differential equation (PDE)-constrained-optimization approach, where we seek to minimize the misfit between the recorded time-domain response at the pile head (the IR data), and the response due to trial distributions of the spatially varying soil stiffness, subject to the coupled pile–soil wave propagation physics. We report numerical experiments involving layered soil profiles for piles founded on either soft or stiff soil, where the inversion methodology successfully characterizes the soil.

Over the years I have been looking at many different aspects of the problem of pile dynamics, which includes both prediction of drivability of piles and the inverse problem of estimating the static resistance of piles based on their performance during driving. In the course of working with all of this many ideas have come to mind; two of those are as follows:

1. Is it possible to use the model (or something like it) in Closed Form Solution of the Wave Equation for Piles for the inverse method? My experience with Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles and its progeny informed me that managing the inverse method in a full FEA model including pile and soil was difficult and getting past uniqueness issues (which have plagued pile dynamics from the start) was next to impossible.
2. Is it possible to use the pile hammer as a geotechnical sounding tool to determine the properties of soil layers into which the pile is being driven? In Improved Methods for Forward and Inverse Solution of the Wave Equation for Piles the soil at any given point was defined by the “Mohr-Coulomb triple” (unit weight, internal friction angle and cohesion) along with other properties, which is the point for most soil testing. The inverse method returned those properties.

The present paper does some interesting things to get to those solutions but ultimately doesn’t quite get to reaching a solution to these problems.

The Strong Point

Probably the strongest point of the paper is the entire mathematical presentation, from the development of the method to its execution. It shows computational proficiency of a high order. For example, it is the first time in pile dynamics that I have seen the use of the conjugate gradient technique. As the product of a PhD program with a heavy emphasis on computational fluid mechanics, this technique was well familiar to me (along with GMRES, which was the method of choice for my colleagues.) One of the challenges the geotechnical industry faces moving forward is the proper application of numerical techniques to geotechnical problems which are non-linear in ways which are unknown in other fields. We have people who are specialists with the geomechanics and people who are specialists in numerical methods, but few are those who are proficient in both.

One thing I would like to mention is that my use of a polytope method–which had many drawbacks–was driven by the difficulties in optimising geotechnical problems. Those difficulties are caused largely by the existence of false minima and maxima in the solution. It is why we still see, for example, grid optimisation used for slope stability problems: the use of, say a Newton’s Method type of optimisation may easily result in finding a false minimum. Although I think the author’s techniques have great promise of solving these problems, it is something they will have to watch for moving forward.

The Soil Property Issue

Probably the greatest weakness of the paper is the way soil properties are characterised.

Let us first consider the system model presented in Closed Form Solution of the Wave Equation for Piles, shown below.

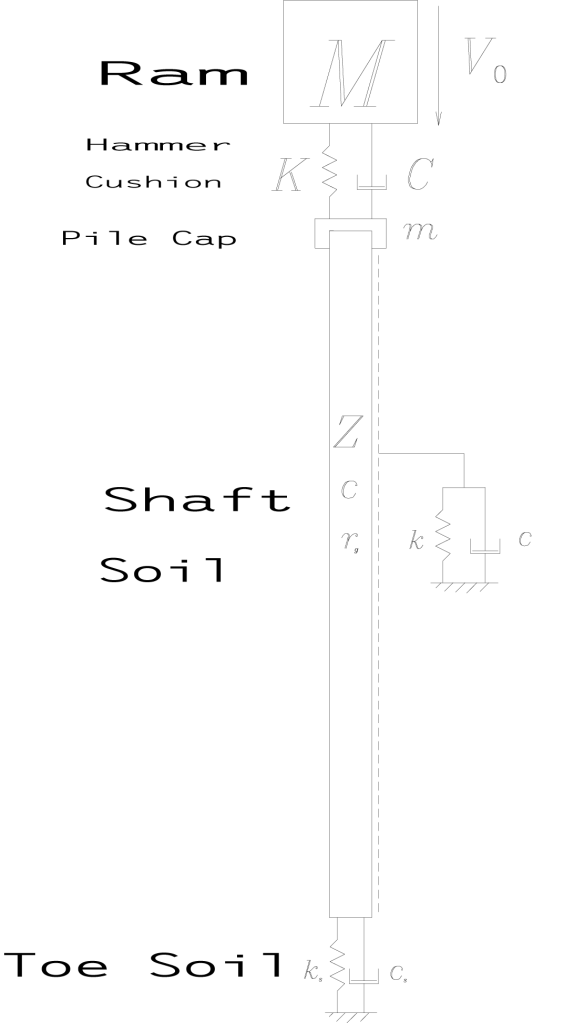
In this diagram the ram mass M impacts the cushion with a velocity V_o. There are several stiffnesses and damping coefficients k and c respectively. The accessory has a mass of m. The pile has an acoustic speed c, an impedance Z and a geometry ratio r_g. For inverse analysis the hammer, cushion and driving accessory can be deleted and a force F(t) and velocity V(t) (both a function of time) substituted at the pile head.

The equation of motion u(x,t), which is a function of both the distance from the pile head x and time t, is given by the equation

(1)

The variables a and b are stiffness and damping related coefficients which are related to k and c by geometric and material property considerations, as discussed in Closed Form Solution of the Wave Equation for Piles.

Although the present paper allows for k(x), the one major difference between the governing equation presented above and the one in the paper is the omission of damping by the latter. (This omission is also repeated at the pile toe.) The soil damping is for the most part a representation of the propagation of wave energy from the pile as it is dynamically loaded. It is impossible to avoid in one form or another. First derivatives like that are always a danger in problems such as this. One way to get around that is to redistribute the damping into the spring and mass terms using Rayleigh damping. This is very frequency dependent and can be tricky to accurately apply; however, if it can be done successfully (and the authors’ note of wavespeed changes with soil interaction may be part of the solution) it would bypass the problems created by the first derivative. (The same comments regarding the shaft also apply at the toe, where an additional mass would have to be applied to achieve Rayleigh damping.)

But that doesn’t address what is, in some ways, the more serious issue: applying a linear model to a very non-linear problem. Concentrating on the shaft resistance, let us begin by noting the results in Estimating Load-Deflection Characteristics for the Shaft Resistance of Piles Using Hyperbolic Strain Softening, and stipulating that, even with hyperbolic stress-strain considerations, up to the time of separation between the shaft and the soil the load-deflection relationship is essentially linear. This study showed that, for the specific case in question, the geometric nonlinearity of the deflecting soil around the shaft and the material nonlinearlity of the soil offset each other to a large degree. Obviously more study needs to be done but this is a start.

Having said that, let us look at a diagram I have used and modified over the years:

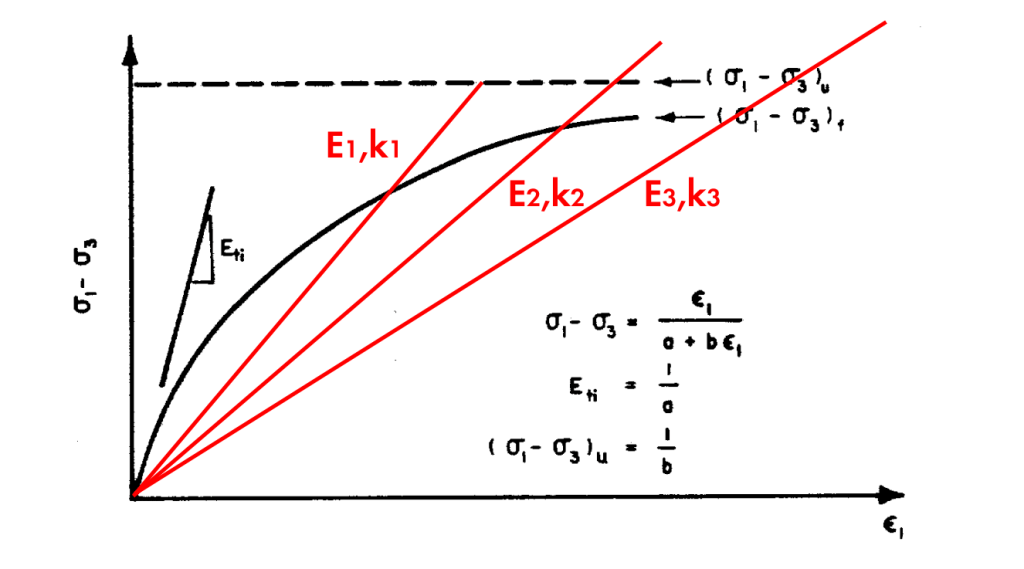
At zero strain we have the small strain elastic or shear modulus. As strain increases, if we use a linear model for load-deflection the only way the model can simulate that kind of response is to do some kind of “secant modulus” estimate. What this means is that the elastic modulus/shear modulus/spring constant is strain dependent, which will vary with loading condition (to put it in classical geotechnical terms, to what extent the shaft resistance is mobilised.) It is also worth noting that this mobilisation is not identical in static and dynamic testing, even on the same pile.

Based on all of this, it is difficult to see how the results of the inverse method can be used to accurately characterise the load-deflection characteristics of the pile, let alone the properties of the soil.

I should note that quite a few of my comments in Comments on “Fictitious soil pile model for dynamic analysis of pipe piles under high-strain conditions” apply to this situation as well. This linearity problem is a major reason why I never have attempted to use the model in Closed Form Solution of the Wave Equation for Piles as a “full-up” inverse method.

Conclusion

This paper is an interesting study of the problem at hand. While some significant advances have been done in the numerical treatment of the problem, the physics of the pile-soil system need to be re-examined and improved.